 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)

| 
| 
| … |

| 
| 
| … |


1)  - с вырожденным распределением, т.е.
- с вырожденным распределением, т.е.  .
.
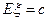


| ||

| 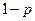
| 
|
2)  - с распределением Бернулли:
- с распределением Бернулли:


3)  - с биномиальным распределением.
- с биномиальным распределением.
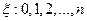 ;
;  (
( - можно рассматривать как число успехов в
- можно рассматривать как число успехов в  независимых испытаниях Бернулли).
независимых испытаниях Бернулли).

| ||

| 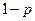
| 
|
Введем случайные величины  - независимые одинаково распределенные случайные величины,
- независимые одинаково распределенные случайные величины,
 , где
, где  - можно интерпретировать как число успехов в
- можно интерпретировать как число успехов в 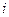 -ом испытании
-ом испытании 
 - число успехов во всех
- число успехов во всех  испытаниях.
испытаниях.
Имеем,
 ; и
; и  ;
;
Распределение у  и у
и у  одинаковое
одинаковое 
 и
и  .
.
 ;
; 
2-ой способ вычисления (по определению): 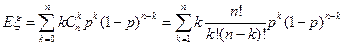 =
=
 = {где
= {где  =
= 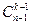 }
} 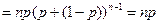 ;
;
 =
=  =
=
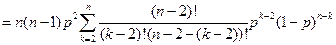
 =
=
=  ;
;

4) 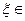 П
П  - распределение Пуассона
- распределение Пуассона
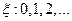 и
и 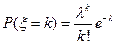
Вычисляем:
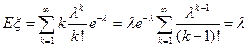

 =
=  +
+  =
=

 .
.
II.  - с абсолютно непрерывным распределением,
- с абсолютно непрерывным распределением,  - плотность;
- плотность;


1) 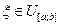
Это означает, что: 
 ;
;
 ;
;
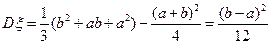 .
.
2)  - с распределением Коши;
- с распределением Коши; 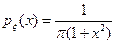
 - расходится (так как интегрируемая функция в
- расходится (так как интегрируемая функция в 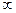 ~
~  );
);
Математическое ожидание отсутствует.
3)  - с нормальным (гауссовским) законом распределения с параметрами
- с нормальным (гауссовским) законом распределения с параметрами  ,
, 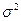 , где
, где  ,
,  .
.
Обозначение: 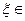
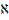
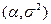
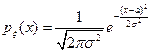
 = { пусть
= { пусть  } =
} = 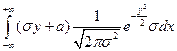 =
=
=  .
.
Здесь 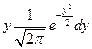 - нечетная функция по симметричному относительно 0 множеству, интеграл сходится
- нечетная функция по симметричному относительно 0 множеству, интеграл сходится 
 = 0; а
= 0; а  = 1 как интеграл от плотности по всей прямой.
= 1 как интеграл от плотности по всей прямой.
И, следовательно,  .
.
Далее,
 = { пусть
= { пусть  } =
} = 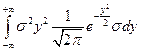 =
=
=  .
.
Вопрос: чему равна дисперсия разности независимых случайных величин?
Имеем: 


Дисперсия разности – это НЕ разность дисперсий.
Лекция 10 (9.11.10)
Поиск по сайту: