 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Свойства операции транспонирования матриц
1) 
2) 
3) 
Умножениематриц.
Умножение матрицы A на матрицу B определено, когда число столбцов матрицы A равно числу строк матрицы B (условиесцепления).В этом случае матрица A называется согласованной с матрицей B.
Определение Произведениемматриц A размера 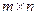 и B размера
и B размера  называется матрица С, элементы которой
называется матрица С, элементы которой  равны скалярным произведениям векторов-строк
равны скалярным произведениям векторов-строк  матрицы A на векторы-столбцы
матрицы A на векторы-столбцы 
 матрицы B:
матрицы B:
С = AB = 
 Матрица С имеет размер
Матрица С имеет размер 
Пример. A =  B =
B =  .
.
A 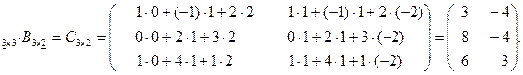
Свойствапроизведенияматриц.
1) Произведениевектора-строки  , наматрицу
, наматрицу  eсть вектор-строка
eсть вектор-строка  , где
, где 
Пример.

2) Произведениематрицы 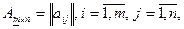 навектор-столбец
навектор-столбец  есть вектор-столбец
есть вектор-столбец  где
где 
Пример.


3) Произведениевектора-столбца  навектор-строку
навектор-строку  есть матрица
есть матрица 
Пример.

4) Произведениевектора-строки  навектор-столбец
навектор-столбец  есть число (или матрица размера 1
есть число (или матрица размера 1  1)
1) 
Пример. 
5) Свойства произведения матриц. Пусть  - матрицы соответствующих размеров (чтобы произведения матриц были определены). Тогда:
- матрицы соответствующих размеров (чтобы произведения матриц были определены). Тогда:
a) (AB)C = A(BC);
b) (A+B)C = AC+BC;
c) A(B+C) = AB+AC
d) 
e) AI = A;
f) IA=A;
g) 
h) 
6) Произведение матриц, вообще говоря, некоммутативно, т.е.  .
.
Для квадратных матриц А и В одного порядка матрица [A,B]=AB - BA называется коммутаторомматриц А и В.
7) Существуют делителинулевойматрицы, т.е. из  и
и 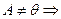
 и из
и из  и
и 
 .
.
8) В общем случае из того, что AB = AC и A 
9) Транспонированиепроизведения. Пусть 
 Тогда
Тогда 
 - условие сцепления выполняется только для
- условие сцепления выполняется только для 
10) Определительпроизведенияквадратныхматриц одного порядка detAB=detA  detB.
detB.
Возведение матрицвнатуральнуюстепень.
Определение Натуральнойстепенью An, n  , квадратной матрицы А называется произведение n матриц, равных А, т.е An
, квадратной матрицы А называется произведение n матриц, равных А, т.е An 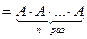 .
.
Свойстваоперациивозведениявнатуральнуюстепень.
1) 
2) 
Матрица называется нильпотентной, если  для некоторого
для некоторого  Наименьшее из чисел m, для которых имеет место это равенство, называется индексомнильпотентности.
Наименьшее из чисел m, для которых имеет место это равенство, называется индексомнильпотентности.
Матрица А называется идемпотентной, если 
Матрица А называется инволютивной, если A  .
.
Многочлены отматриц.
Пусть даны квадратная матрица  и многочлен f(x) =
и многочлен f(x) = 
 .
.
Значением многочлена f(x) при x=A или многочленом f(A) совпадает с порядком матрицы А.
Если  то многочлен f(x) называется аннулирующим многочленом матрицы А, а сама матрица А- корнем многочлена f(x).
то многочлен f(x) называется аннулирующим многочленом матрицы А, а сама матрица А- корнем многочлена f(x).
Пример. 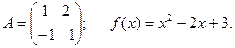

Матрица A является корнем f(x), а f(x) является аннулирующим многочленом для матрицы А.
4. Обратная матрица.
Определение. Квадратная матрица А называется вырожденной (невырожденной), если detA=0 (detA  0).
0).
Определение. Матрица 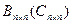 называется правой (левой) обратной к матрице
называется правой (левой) обратной к матрице  , если АВ=I (CA=I).
, если АВ=I (CA=I).
Теорема. Если для матрицы А  существуют левая обратная матрица С и правая обратная матрица B, то С=B.
существуют левая обратная матрица С и правая обратная матрица B, то С=B.
Доказательство.
С=CI=C(AB)=(CA)B=IB=B.
Определение. Матрица  называется обратной по отношению к квадратной матрице A, если при умножении матрице A
называется обратной по отношению к квадратной матрице A, если при умножении матрице A  на данную матрицу А как справа, так и слева, получается единичная матрица: A
на данную матрицу А как справа, так и слева, получается единичная матрица: A 
Понятие о необходимом и достаточном условиях.
Любую теорему можно записать в виде: 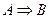 , где А-условие теоремы а B- её заключение. Высказывание В называется необходимым условием для А, а высказывание достаточным условием для В.
, где А-условие теоремы а B- её заключение. Высказывание В называется необходимым условием для А, а высказывание достаточным условием для В.
Если высказывания А и В таковы, что  (каждое следует из другого), то говорят, что каждое из этих условий является необходимым и достаточным условием другого и пишут
(каждое следует из другого), то говорят, что каждое из этих условий является необходимым и достаточным условием другого и пишут  .
.
Необходимое и достаточное условие существования обратной матрицы.
Обратная матрица  существует и единственна тогда и только тогда, когда исходная матрица является невырожденной.
существует и единственна тогда и только тогда, когда исходная матрица является невырожденной.
Пример. Вычислить для матрицы А матрицу  , пользуясь определением обратной матрицы.
, пользуясь определением обратной матрицы.

Решение.
detA=18-20=-2. Следовательно обратная матрица  существует.
существует.
Пусть  , тогда, по определению обратной матрицы,
, тогда, по определению обратной матрицы, 





Таким образом, обратная матрица имеет вид: 
Проверим выполнение условия А 

Итак, 
Свойства обратной матрицы.
Если detA  0 и detВ
0 и detВ  0, то:
0, то:

Вычисление обратной матрицы.
Пусть  . Тогда
. Тогда  где матрица С имеет вид:
где матрица С имеет вид: 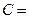

Матрица С называется союзной или присоединённой по отношению к матрице А. Элемент  матрицы с равен алгебраическому дополнению Aji элемента
матрицы с равен алгебраическому дополнению Aji элемента  исходной матрицы А,
исходной матрицы А, 
Пример. Найти матрицу, обратную к матрице 
Решение. det A=6-4=2 
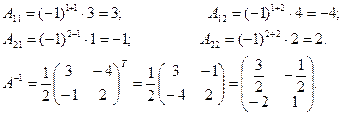
5. Ранг матрицы. Базисный минор.
Рассмотрим матрицу m x n  Выделим из этой матрицы r строк и r столбцов. Элементы, стоящие на пересечении этих строк и столбцов, образуют матрицу размерами rxr. Определитель полученной матрицы называется минором r-го порядка.
Выделим из этой матрицы r строк и r столбцов. Элементы, стоящие на пересечении этих строк и столбцов, образуют матрицу размерами rxr. Определитель полученной матрицы называется минором r-го порядка.
Определение . Рангом матрицы А называется целое число r, если у матрицы есть минор r-го порядка, от личный от нуля, а все миноры (r+1)-го порядка равны нулю. Минор r-го порядка называется базисным минором Мб. Ранг матрицы обозначается rangA=r.
Если существует элемент матрицы, отличный от нуля, то ранг матрицы не меньше 1. Если все элементы матрицы равны 0, то ранг матрицы равен 0. Если у квадратной матрицы основной определитель detA отличен от нуля, то rangA=n. У матрицы может быть несколько базисных миноров, но с одним и тем же рангом.
Столбцы и строки, на пересечении которых стоят элементы базисного минора, называются базисными столбцами (строками).
Любой столбец (строка) матрицы А является линейной комбинацией ее базисных столбцов (строк).
Ранг матрицы не меняется
- при перемене местами двух строк (столбцов)
- при умножении строки на число, не равное нулю
- при транспонировании
- при линейном преобразовании.
Поиск по сайту: