Ускорение

В некоторый момент времени t₀ материальная точка находится в положении А и имеет скорость 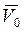, а через некоторое время 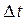в момент t₁ = t₀ + - в положении В и имеет скорость (рис. 1.30). Если вектор перенести в точку А (обозначено пунктиром на рис. 1.30), а через концы векторов 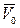и 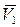провести новый вектор 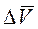, то получим векторное равенство

. (1.34)

Рис. 1.30

Среднее ускорение движения - это изменение скорости материальной точки за промежуток времени, в течение которого это изменение произошло:

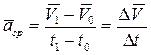(1.35)

Мгновенное ускорение (в дальнейшем, просто ускорение) – это предел среднего ускорения при бесконечном уменьшении промежутка времени наблюдения, т. е.

. (1.36)

Таким образом, ускорение – это первая производная от скорости или вторая производная от закона движения по времени (четвертая характеристика движения). Ускорение является векторной величиной и ее направление совпадает с направлением вектора в его предельном положении, т. е. вектор ускорения всегда располагается с той стороны от касательной к траектории движения, что и сама траектория.

Аналогично скорости компоненты вектора ускорения можно представить через компоненты вектора скорости и компоненты радиус – вектора положения точки:

, (1.37)

В этом случае модуль ускорения можно определить как:

(1.38)

Движение материальной точки определяется четырьмя основными характеристиками: законом движения, траекторией, скоростью и ускорением.

1.2.2. Естественный способ задания движения

Данный способ применяется только в том случае, когда известна траектория движения.

Для задания движения применяется прямоугольная естественная система координат (рис. 1.31), которая характеризуется тем, что:

- начало координат всегда совпадает с положением материальной точки;

- первая ось (ось τ) всегда располагается на касательной к траектории движения и направлена в ту сторону, куда движется материальная точка (касательная);

- вторая ось (ось η) всегда располагается на нормали к траектории движения (всегда перпендикулярна касательной к траектории и находится в плоскости движения (если движение пространственное - то в соприкасающейся плоскости) и направлена в сторону вогнутости траектории (нормаль);

- третья ось (ось β) всегда располагается на бинормали к траектории (т.е. перпендикулярна и касательной, и нормали) и направлена так, чтобы образовывать с первой и второй осью правую систему координат (бинормаль).

Рис. 1.31.

Зависимость расстояния по времени от текущего положения точки до некоторого начального, измеренного вдоль траектории, S(t) является естественным законом движения.

В этом случае для скорости справедливо соотношение:

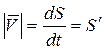, (1.39)

Разложив по осям вектор скорости 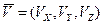в естественной системе координат, получим:

, (1.40)

Вектор скорости проецируется только на одну ось – ось τ.

А вектор ускорения будет проецироваться только на две оси - ось τ и ось η, а третья проекция .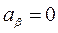

Величины проекций ускорения и определяются по системе уравнений:

, (1.41)

где 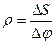- радиус кривизны траектории.

Связь между компонентами скоростей и ускорений

Поскольку вектора скорости и ускорения в каждый момент времени определяются равнозначно, то между их компонентами при разложении в различных системах координат будут иметь место следующие зависимости:

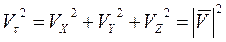, (1.42)

, (1.43)

Дифференцируя первое из приведенных выражений получаем:

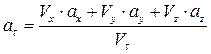. (1.44)

Поиск по сайту: