Симметричный оптимум

Одна из задач настройки системы на ТО — сделать контур регулирования астатическим. Этого достичь не удается, если в состав объекта регулирования входит интегрирующее звено. Тогда стремятся получить передаточную функцию системы, ЛАЧХ которой на частоте среза сохраняет свойственный для ТО наклон –20 дБ/дек и меняет этот наклон до –40 дБ/дек в области низкой 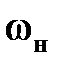и высокой 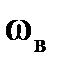частот пропускания, отличающихся от частоты среза не менее чем в два раза.

Одним из вариантов таких САУ являются системы, настроенные на симметричный оптимум (СО) [9, 10]. При этом передаточная функция разомкнутой цепи для САУ, обеспечивающих характеристики СО, имеет вид:

.

(13.5)

Известно, что для системы, настроенной на СО, перерегулирование составляет около 43 - 45 %. Тогда, согласно номограммам Солодовникова, время переходного процесса можно оценить по соотношению:

.

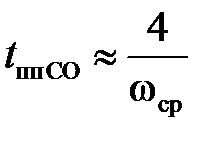(13.6)

На рис. 13.3 приведена ЛАЧХ для САУ, передаточная функция разомкнутой цепи которой представлена выражением (13.5). Для нее , и 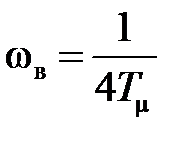, поэтому, в соответствии с (13.6), 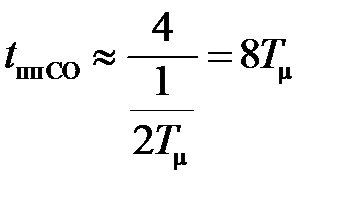, отсюда

.

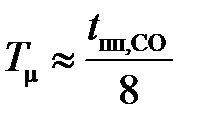(13.7)

Рис. 13.3. ЛАЧХ системы, настроенной на СО

Следует отметить, что запас устойчивости по амплитуде 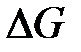для систем, настроенных на ТО или СО, равен бесконечности, т.к. их фазовые характеристики никогда не достигают значения –180°. Запасы устойчивости по фазе соответственно равны 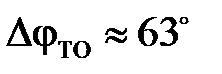и .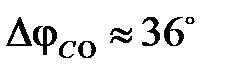

Если САУ, настроенную на СО, замкнуть инерционной обратной связью с коэффициентом передачи и постоянной времени , то ее передаточная функция будет иметь вид

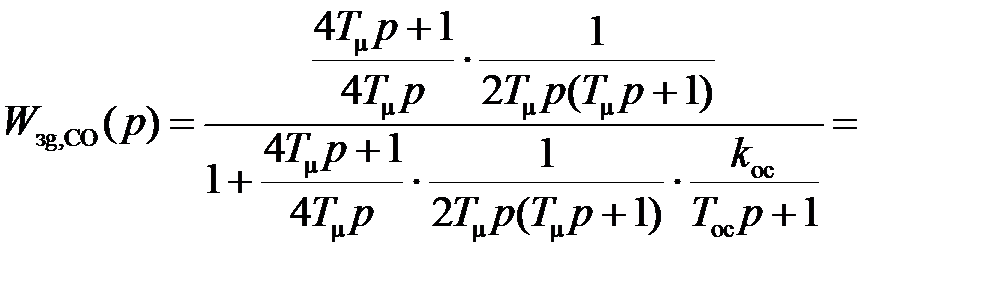
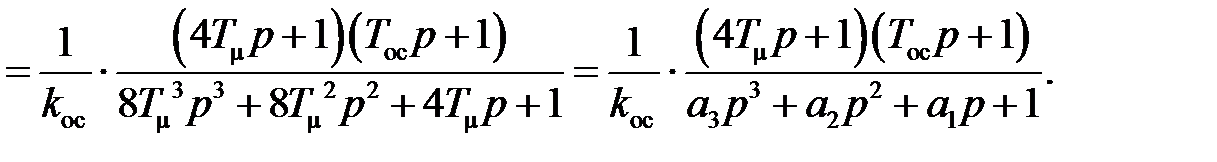
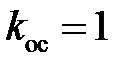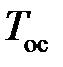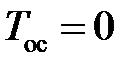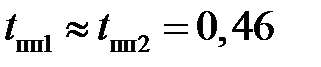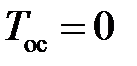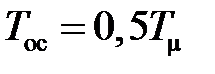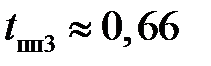На рис. 13.5 приведены переходные характеристики САУ, настроенной на СО, при единичном входном воздействии, , с и различных значениях . При (кривая 3) перерегулирование составляет около 49,5 %, при (кривая 2) — около 45 %, при (кривая 1) — около 43 %. Время переходного процесса с при и при , с при .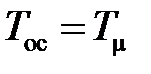

Рис. 13.4. Переходные характеристики САУ, настроенной на СО, при различной инерционности цепи ее обратной связи

Таким образом, постоянная времени в цепи обратной связи САУ, настроенной на какой-либо оптимум, приводит к увеличению перерегулирования, и при 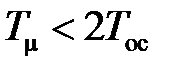существенно снижается быстродействие САУ.

Обеспечение оптимальных показателей качества регулирования в динамических режимах (настройка САУ на ТО или СО) достигается в результате структурно-параметрического синтеза корректирующих устройств. Рассмотрим решение этой задачи на конкретном примере.

Пример

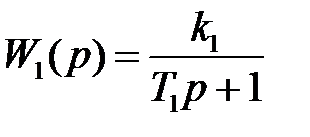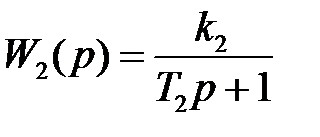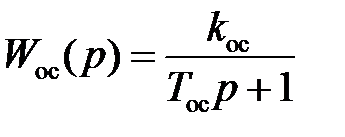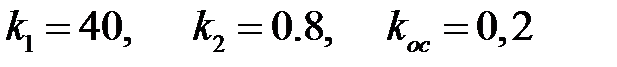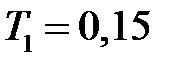Произвести настройку внутреннего контура (рис.13.5) двухконтурной САУ на технический оптимум при следующих параметрах: , , , где , с, с, с. При этом необходимо обеспечить время переходного процесса с.

Рис. 13.5. Структурная схема внутреннего контура двухконтурной САУ

Передаточная функция разомкнутой цепи нескорректированной системы будет равна

.

Исходя из соотношения (13.2) определим значение эквивалентной некомпенсируемой постоянной времени 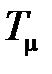по формуле

,

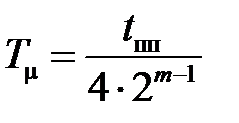где 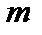— общее количество контуров регулирования.

При 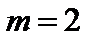получим

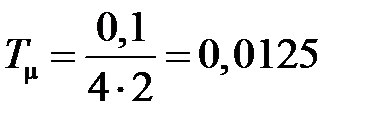с.

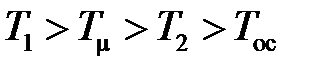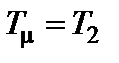Таким образом, , и в качестве эквивалентной некомпенсируемой постоянной времени выбираем ближайшую к расчетному значению меньшую постоянную времени нескорректированной САУ. Таковой в данном случае является постоянная времени с, поэтому пусть . Тогда для САУ, настроенной на ТО, в соответствии с (6.6) будем иметь

,

.

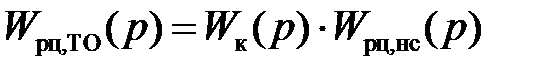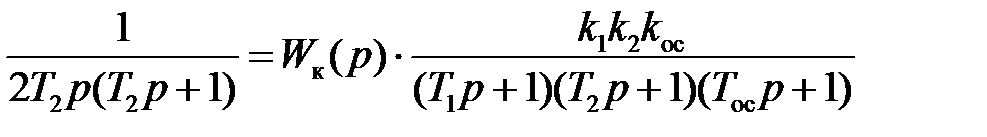Отсюда передаточная функция корректирующего устройства

,

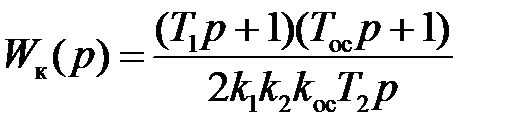т.е. корректирующее устройство является ПИД-регулятором с передаточной функцией 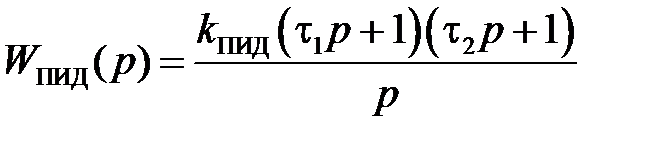, у которого

, .

Поскольку отношение , то переходная характеристика замкнутой скорректированной САУ будет иметь вид, близкий к кривой 2 на рис. 6.9, перерегулирование не превысит 5 % и заданное быстродействие системы будет обеспечено.

Настройка САУ на симметричный оптимум производится аналогично. При этом для многоконтурной системы эквивалентная некомпенсируемая постоянная времени рассчитывается по формуле 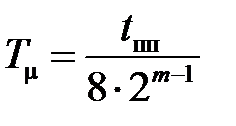, а корректирующее устройство будет более сложным и, как правило, состоит из нескольких последовательно соединенных типовых регуляторов.

Контрольные вопросы

1. Запишите передаточную функцию разомкнутой цепи системы, настроенную на технический оптимум.

2. Запишите передаточную функцию разомкнутой цепи системы, настроенную на симметричный оптимум.

3. Назовите величины перерегулирования для систем, настроенных на симметричный и технический оптимумы.

4. Что такое 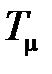в выражениях передаточных функций разомкнутой цепи системы?

5. Какие запасы по фазе и амлитуде для систем настроенных на технический и симметричный оптимум?

6. Поясните алгоритм настройки системы на оптимум.

Поиск по сайту: