 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Формулы приближенного дифференцирования, основанные на первой итерационной формуле Ньютона
Пусть имеем функцию y(x), заданную в равноотстоящих точках 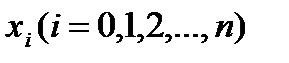 отрезка [a,b] с помощью значений
отрезка [a,b] с помощью значений 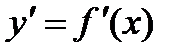 ,
, 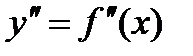 и т.д. Функцию y приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов x0, x1,…,
и т.д. Функцию y приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов x0, x1,…,  .
.
Имеем:
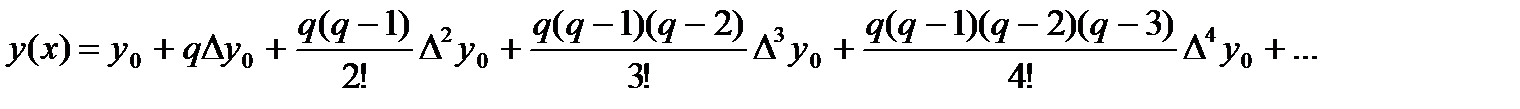 (1)
(1)
Где:
 и
и  (i=0,1,…)
(i=0,1,…)
Производя перемножение биномов, получим:
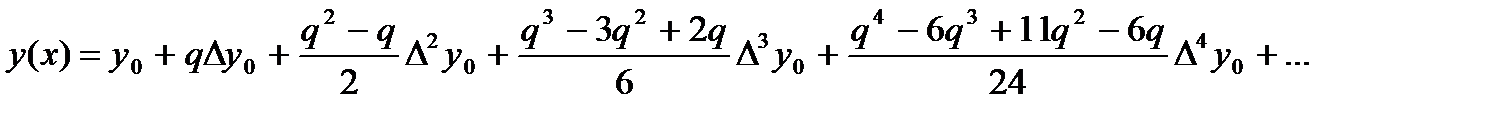 (
(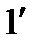 )
)
Так как
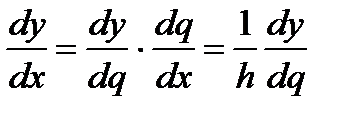
То
 (2)
(2)
Аналогично, так как:
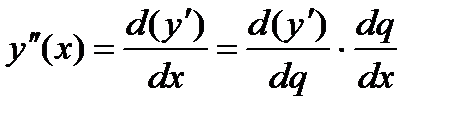
То
 (3)
(3)
Таким же способом в случае надобности можно вычислить и производные функции y(x) любого порядка.
Заметим, что при нахождении производных  в фиксированной точке x в качестве x0 следует выбирать ближайшее табличное значение аргумента.
в фиксированной точке x в качестве x0 следует выбирать ближайшее табличное значение аргумента.
Иногда требуется находить производные функции у в основных табличных точках xi. В этом случае формулы численного дифференцирования упрощаются. Так как каждое табличное значение можно считать за начальное, то положим x=x0, q=0; тогда будем иметь:
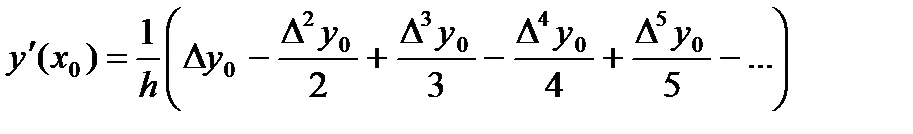 (4)
(4)
И  (5)
(5)
Если 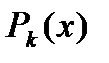 - интерполяционный полином Ньютона, содержащий разности
- интерполяционный полином Ньютона, содержащий разности  и
и 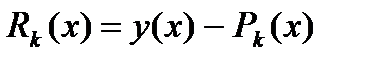 - соответствующая погрешность, то погрешность в определении производной есть:
- соответствующая погрешность, то погрешность в определении производной есть:
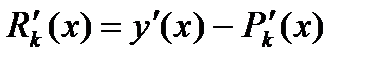
Как известно,
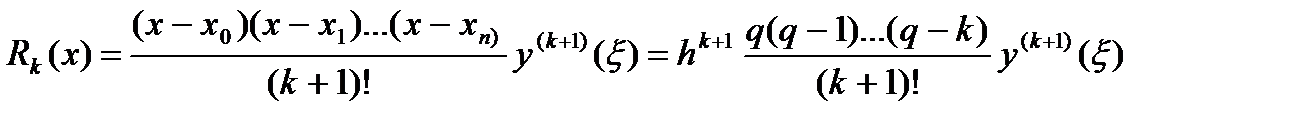
Где 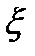 - некоторое промежуточное число между значениями x0, x1,…, xk, x. Поэтому, предполагая, что
- некоторое промежуточное число между значениями x0, x1,…, xk, x. Поэтому, предполагая, что 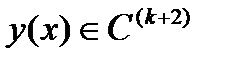 , получим:
, получим:
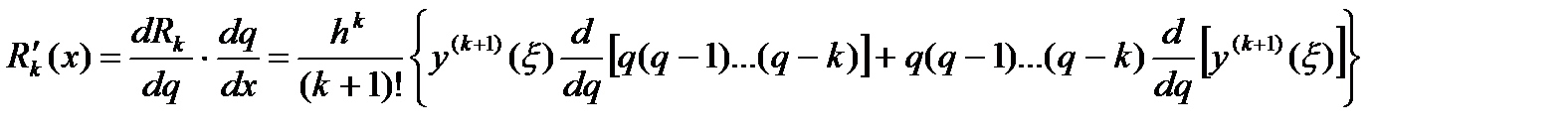
Отсюда при x=x0 и, следовательно, при q=0 и учитывая, что  , будем иметь:
, будем иметь:
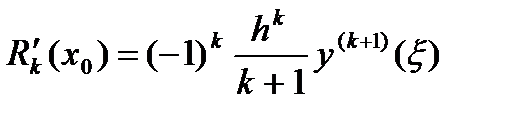 (6)
(6)
Так как 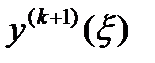 во многих случаях трудно оценить, то при h малом приближенно полагают:
во многих случаях трудно оценить, то при h малом приближенно полагают:
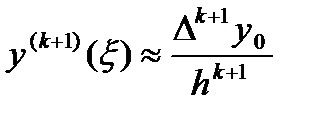
и, следовательно:
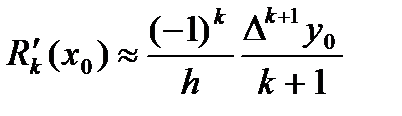 (7)
(7)
Аналогично может быть найдена погрешность 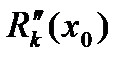 для второй производной
для второй производной 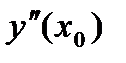 .
.
Пример 1. Найти 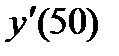
Значения функции 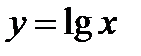
| x | y | ∆y | ∆2y | ∆3y |
| 1,6990 | -36 | |||
| 1,7404 | -31 | |||
| 1,7782 | ||||
| 1,8129 |
Решение: Здесь h=5. Дополним таблицу 60 столбцами конечных разностей (десятичные разряды, как обычно, не указываются; они определяются десятичными разрядами значений функции).
Используя первую строчку таблицы, на основании формулы (4), с точностью до разностей третьего порядка, будем иметь:
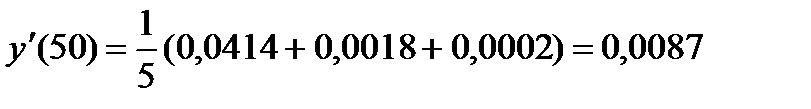
Для оценки точности найденного значения заметим, что, так как табулирования выше функция есть 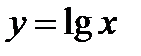 , то
, то
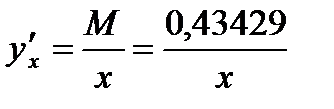
Следовательно:
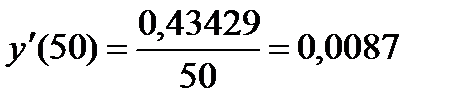
Таким образом, результаты совпадают с точностью до четвертого десятичного знака.
Запишем в явном виде формулы для первой производной в угловых точках по формуле (4) выражая все конечные разности через значения функции в углах; учтем значение погрешности (6).
1. Для двух точек (n=2) – линейный полином

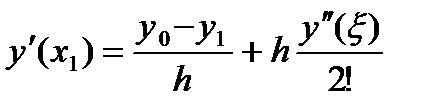
Говорят, что эта формула имеет первый порядок точности относительно шага h, где h=x1-x0 – расстояние между точками.
По формуле (12) в точках x0, x1, x2
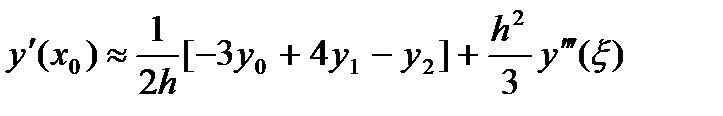 (2.44а)
(2.44а)
Второго порядка точности
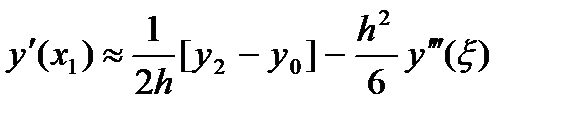 (2.44б)
(2.44б)
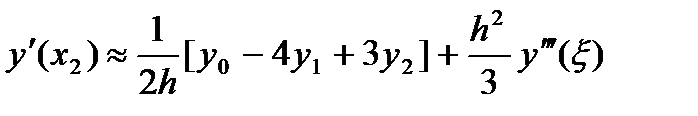 (2.44в)
(2.44в)
2. n=3 (четыре точки)

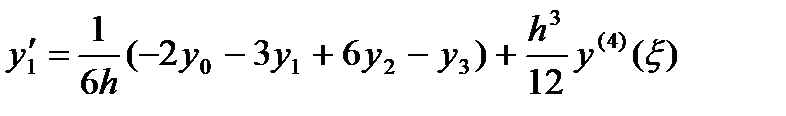
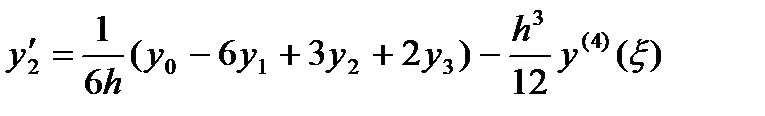

3. n=4 (пять точек)
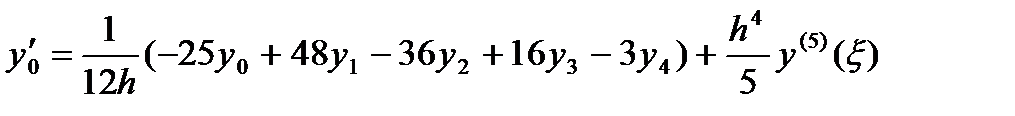

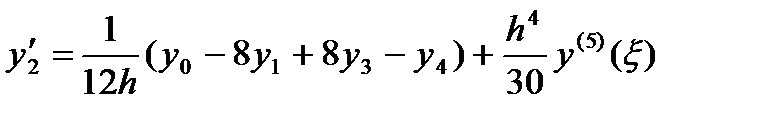
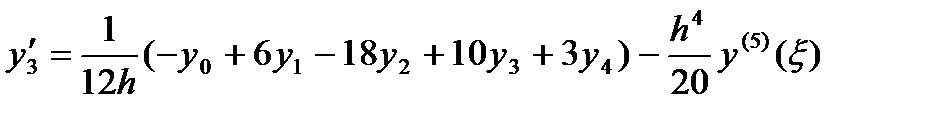
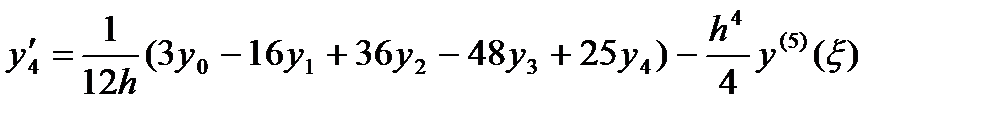
Рассмотрение формул 1-3 показывает, что если число точек нечетно и производная берется в средней точке, то соответствующая формула численного дифференцирования выражается более просто и обладает повышенной точностью.
Для повышения точности аппроксимации производных теоретически следует увеличивать степень интерполяционного многочлена – число точек.
Аналогично можно вывести формулы для производной второго порядка:
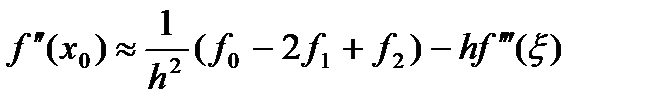 (2.45а)
(2.45а)
 (2.45б)
(2.45б)
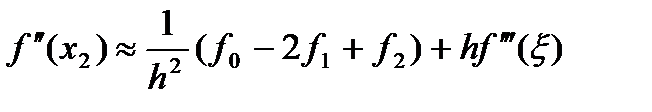 (2.45в)
(2.45в)
Вторая производная по формулам (2.45а)—(2.45в) в крайних точках x0 и х2 аппроксимируется с первым порядком точности, а в центральной х1 — со вторым. В центральных точках производные аппроксимируются более точно, чем в крайних, что видно из рисунка 2.4 и следует также из приведенных формул. Аппроксимация производных в крайних точках используется при численном решении задачи Коши и краевых задач для обыкновенных дифференциальных уравнений и уравнений в частных производных.
Запишем полиномы для неравноотстоящих точек.
Линейным полином (две точки):
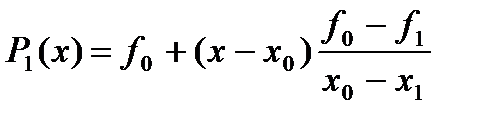 (9)
(9)
Квадратичный полином (три точки):
 (10)
(10)
Из формул (9) и (10) с использованием выражения (8) получаем, дифференцируя x,
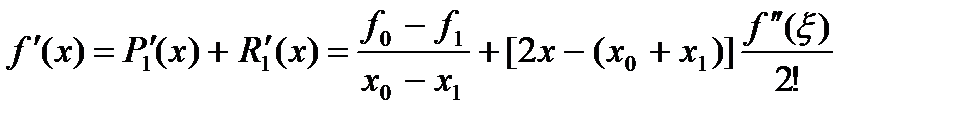 (11)
(11)
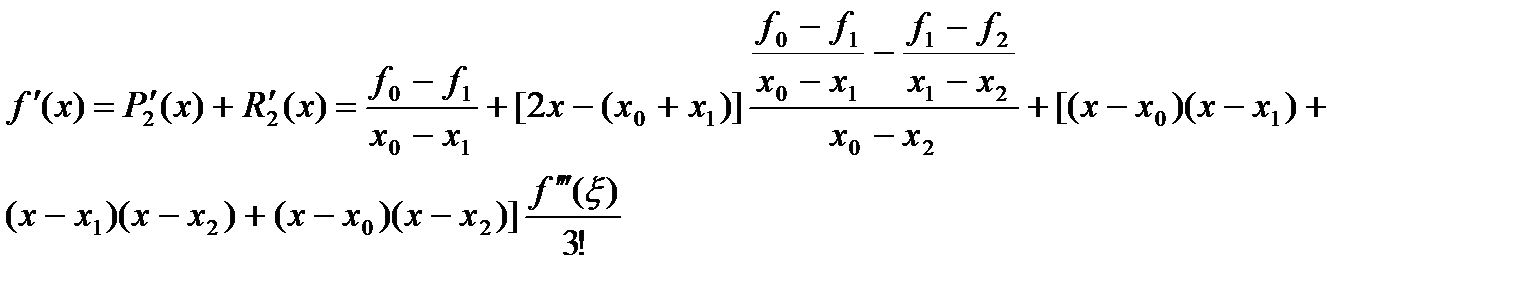 (12)
(12)
Формулы (11) и (12) дают значения первой производной в случае неравноотстоящих узлов, при этом формула (11) получена дифференцированием интерполяционного многочлена первой степени, а (12) — многочлена второй степени с учетом формул для погрешностей интерполяции. Рассмотрим более подробно эти формулы. Очевидно, что при таблично заданных функциях с использованием интерполяционных многочленов производные вычисляются как производные от интерполяционных многочленов соответствующих порошков. Приближенное значение первой производной по формуле (11), полученное дифференцированием  равно:
равно:
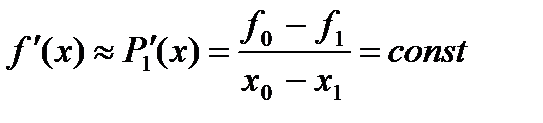
Для вычисления второй производной, очевидно, нужно использовать интерполяционный многочлен Ньютона второй степени. Имеем
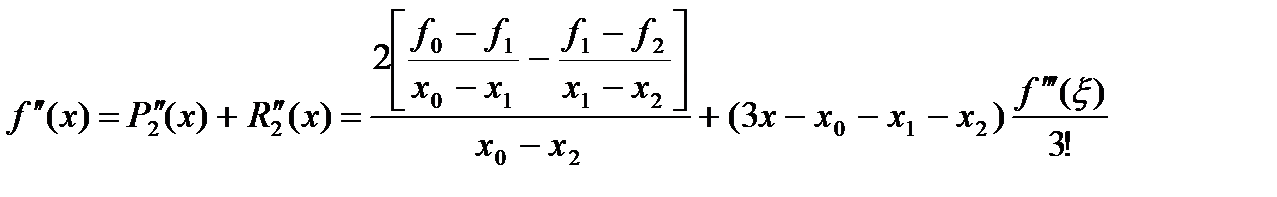 (13)
(13)
Таким образом, приближенное значение второй производной на отрезке [x0, x2] является постоянной, равной
 (14)
(14)
Поиск по сайту: