Турбулентное течение. Критерии гидродинамического подобия

Ламинарное течение жидкости является стационарным. При увеличении скорости течения наступает момент, когда характер течения резко изменяется. Оно становится нестационарным, т. к. скорость частиц жидкости в каждой точке её пространства всё время беспорядочно изменяется. Такое течение называется турбулентным. При этом происходит перемешивание всех слоёв жидкости.

При таком течении жидкости описать её движение довольно затруднительно, т. к. вместо относительно простого уравнения Эйлера (3) приходится решать систему очень сложных дифференциальных уравнений в частных произвольных. Поэтому для качественного описания перехода ламинарного течения в турбулентное применяют метод, основанный на теории подобия.

Два физических процесса называются подобными, если они подчиняются одним и тем же физическим законам. При этом величины, характеризующие подобные явления, получаются путём умножения их на так называемые числа подобия - безразмерные величины, одинаковые для всех однородных величин.

В основе теории подобия лежат 3 теоремы:

1) для двух подобных процессов числа подобия попарно равны друг другу;

2) числа подобия связаны друг с другом уравнениями подобия, являющимися безразмерным решением рассматриваемой задачи;

3) два процесса подобны, если их числа подобия попарно равны.

Эта теория является научной основной экспериментальных исследований сложных явлений.

Основными числами подобия в механике жидкостей и газов являются 4 числа: число Рейнольдса 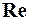, число Фруда 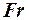, число Струхаля 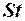, число Маха 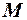. В качестве примера рассмотрим использование числа .

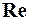Рейнольдс установил, что характер течения жидкости определяется значением безразмерной величины

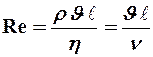
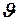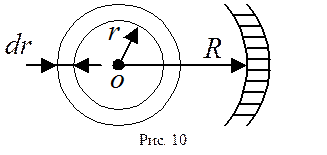
где - плотность жидкости (газа), - средняя по сечению трубы скорость потока, 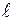- характерный для поперечного сечения размер (например, для квадратного сечения трубы - это сторона квадрата, для круглого сечения - это радиус трубы и т. п.).

При малых значениях числа 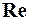течения носит ламинарный характер. Начиная с некоторого , называемого критическим, течение приобретает турбулентный характер. Так для трубы круглого сечения при её характерном размере, равном радиусу, .

Число 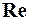служит критерием подобия для течения жидкостей в трубах, каналах и др. Например, характер течения жидкости в круглых трубах разных радиусов будет одинаков, если каждой трубе будет соответствовать одно и тоже число .

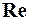Т. образом, число 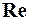выражает соотношение между силами трения и давления жидкости. При определении сил, действующих на тело в потоке жидкости или газа, число 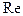служит критерием подобия и в этом случае.

В частности, как установил Стокс, при небольших 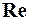, когда сопротивление жидкости или газа, обусловлено только силами трениями, то модуль силы сопротивления среды движению тела в ней будет:

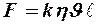- формула Стокса,

где 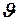- скорость движения тела, 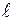- характерный размер тела, 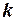- коэффициент пропорциональности, определяемый формой тела. Например, для тела в форме шара 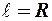, тогда 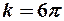, т. е. .

Поиск по сайту: