 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Для решения задачи 2
Необходимо изучить темы «Обобщающие показатели» и «Показатели вариации».
Во втором и третьем вариантах для решения задачи 2 необходимо уяснить отличия и возможности применения средней арифметической и средней гармонической величины.
Перед решением задачи надо ясно представить себе экономический смысл исходных данных в каждом периоде отдельно, а также тех показателей, которые не известны.
Если в искомом показателе отсутствует числитель, он находится как произведение, и, следовательно, используется средняя арифметическая взвешенная

Если в таком показателе отсутствует знаменатель, он находится как частное от деления, и, следовательно, используется средняя гармоническая взвешенная величина

Рассмотрим пример:
Имеются следующие данные о продаже огурцов на трех рынках города за 2 месяца.
| Рынки города | Август | Сентябрь | ||
| Цена за 1 кг., руб. | Продано, кг. | Цена за 1 кг.,руб. | Продано на сумму, тыс. руб. | |
| 5,0 | 6,0 | 28,2 | ||
| 5,5 | 6,5 | 26,0 | ||
| 4,5 | 5,0 | 30,0 |
Необходимо определить среднюю по трем рынкам цену огурцов в августе и сентябре.
Рассуждаем следующим образом:
по смыслу показателя средняя цена определяется делением стоимости товара на его количество. В августе известна цена 1 кг. огурцов и количество проданных огурцов. Следовательно, неизвестна стоимость товара (числитель). Ее можно найти, умножив цену на количество товара. Следовательно, для нахождения средней по трем рынкам цены 1 кг огурцов надо использовать формулу средней арифметической взвешенной (формула приведена выше), где Х- цена 1 кг. огурцов на каждом рынке, а f- количество огурцов, проданных на каждом рынке. В сентябре - не известно количество проданных огурцов (знаменатель). Его можно найти, разделив стоимость товара на цену 1 кг, следовательно, для нахождения средней по трем рынкам цены 1 кг огурцов следует использовать формулу средней гармонической взвешенной (формула приведена выше), где М- стоимость проданных огурцов на каждом рынке, а Х- средняя цена 1 кг огурцов на каждом рынке.
Решение задачи можно представить в табличной форме:
| Рынки города | Август | Сентябрь | ||||
| Цена за 1 кг., руб. | Продано на сумму, тыс. руб. | Количество проданных огурцов, кг. | Цена за 1 кг.,руб. | Продано на сумму, тыс. руб. | Количество проданных огурцов, кг. | |
| Х | f | Х ´ f | Х | М | М/Х | |
| 5,0 | 25,000 | 6,0 | 28,2 | |||
| 5,5 | 24,750 | 6,5 | 26,0 | |||
| 4,5 | 27,000 | 5,0 | 30,0 | |||
| Итого | Х | 76,750 | Х | 84,2 |
Средняя цена 1 кг. огурцов в августе 
Средняя цена 1 кг. огурцов в сентябре

Следовательно, в сентябре 1 кг. огурцов на рынках города стал дороже в среднем на
5,73 руб. - 4,92 руб. = 0,81 руб.
В первом, четвертом, пятом и шестом вариантах для нахождения средней и дисперсии признака, необходимо использовать рациональное решение, т.е. нахождение дисперсии можно упростить, используя формулу:

В интервальных рядах следует сначала найти середину интервала.
Следует помнить, что середина интервала находится путем суммирования крайних значений в группе и делением этой суммы на 2. Если интервал открытый, для установления его примерной величины ориентируются на ближайший интервал, т.е. для первой группы на интервал второй группы, а для последней группы на интервал предпоследней группы. (Исключение: если воображаемый нижний предел первой группы таким образом получается отрицательный, его принимают равным нулю).
Средняя арифметическая находится по формуле:
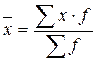
а дисперсия по упрощенной: 
Все расчеты оформить в виде таблицы.
Для нахождения моды и медианы в интервальном ряду распределения (независимо от того равный интервал группировки или неравный) надо использовать следующие формулы:


где х0- нижняя граница модального интервала, i - величина модального интервала, fmo - частота модального интервала, fmo-1 - частота интервала предшествующего модальному, fmo+1 - частота интервала, следующего за модальным. Место нахождения модального интервала - против наибольшей частоты (f).

где х0-нижняя граница медиального интервала, i - величина медиального интервала, Sme-1 - сумма накопленных частот до медианного интервала, fme –
частота медианного интервала. Место нахождения медианного интервала – середина ранжированного ряда определяется по формуле накопленной частоты до самой медианы 
в какую из накопленных частот группировки войдет это значение - там, против нее, находится медианный интервал. Расчет накопленных частот (S) следует оформить дополнительной графой в таблице.
Рассмотрим пример:
Имеются следующие данные о весе пачек чая при проверке его веса с помощью выборочного наблюдения:
| Вес пачек чая, гр. | Количество пачек чая |
| 47-49 | |
| 49-51 | |
| 51-53 | |
| 53-55 | |
| Итого: |
Для нахождения средней и дисперсии делаем расчетную таблицу:
| Вес пачек чая, гр. | Количество пачек (f) | Середина интервала (х) | X ∙ f | X2 ∙ f | Накопленная частота S |
| 47-49 | |||||
| 49-51 | |||||
| 51-53 | |||||
| 53-55 | |||||
| Итого: | Х | Х |
За таблицей находим: 
1.Средню 
2.Дисперсию 
3. Среднее квадратическое отклонение 

 4. Коэффициент вариации
4. Коэффициент вариации 
Следовательно, вариация признака очень незначительная (3,26%) и найденная средняя может достоверно характеризовать совокупность.
Для нахождения моды сначала определяем модальный интервал.
Модальный интервал находится во второй группе, т.к. здесь наибольшее количество пачек чая (52 пачки).
Следовательно, 
Следовательно, в 100 пачках чая больше всего пачек имеющих вес 50 грамм.
Медианный интервал также будет вторым (это совпадение, он может быть и в другой группе, не там, где мода). 
т.е. медианное значение веса пачки чая находится между 50-ой и 51-ой граммовой пачкой в ранжированном ряду (упорядоченном).
Тогда 
(Sme-1=21 пачке, т. к. это количество пачек в группах до медианного интервала. См. Последнюю графу таблицы)
Следовательно, в середине ранжированного ряда находится пачка (пачки) чая, имеющие вес 50,1 грамма.
Поиск по сайту: