 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Напомним формулы кинетических энергий в абсолютном
движении:
¾ материальная точка: 
;
¾ система материальных точек: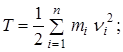 
¾ твердое тело:
¾ при поступательном движении: ;
¾ при вращении вокруг неподвижной оси l: 
¾ при плоско-параллельном движении:
¾при вращении вокруг неподвижной точки:
¾в общем случае движения твердого тела:
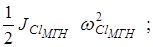
3) Вычислить производные от кинетической энергии, входящие в левую часть уравнений Лагранжа;
4) Определить обобщенные силы, соответствующие выбранным обобщенным координатам (так как каждой обобщенной координате соответствует обобщенная сила, то число обобщенных сил механической системы равно числу обобщенных координат, причем размерность каждой из обобщенных сил соответствует размерности соответствующей обобщенной координаты);
5) Подставить все вычисленные величины в уравнения Лагранжа.
Пример 2.14. Механическая система, показанная на рис.2.13,
состоит из однородного круглого цилиндра 1 массой m1 и радиусом
r, однородного стержня 2 длиной l и массой m2, к которому в точках А и В шарнирно прикреплены ползуны 3 и 4 массами m3 и m4,
также двух пружин, коэффициенты жесткости которых С1 и С2 соответственно. Цилиндр без скольжения катится по горизонтальной плоскости. К нему приложена пара сил с моментом М1 (t).
Рис. 2.13
Пренебрегая сопротивлением качению цилиндра 1, трением в шарнирах и направляющих, а также массой пружин, составить дифференциальные уравнения движения системы.
Решение. Система имеет две степени свободы. В качестве обобщенных координат выберем перемещение q1 = s центра масс С цилиндра 1 и угол q2 = j поворота стержня 2 (против хода часовой стрелки). Полагаем, что при s = 0 и j = 0 пружины не деформированы.
Уравнения Лагранжа второго рода для данной системы имеют вид
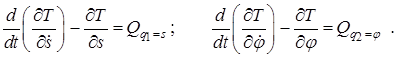(2.42)
Кинетическая энергия системы складывается из кинетических энергий
¾ цилиндра 1 и стержня 2, совершающих плоское движение;
¾ ползунов 3 и 4, совершающих поступательное движение:
T = 
+ 
+ 
+ 
.
Кинетическая энергия цилиндра 1:
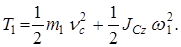Так как 
то
Кинетическая энергия стержня 2:
Скорость центра масс стержня 
где 
¾ МЦС стержня. Принимая во внимание, что 
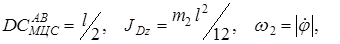получаем
Ползуны движутся поступательно и, следовательно,
Таким образом, кинетическая энергия системы, выраженная через обобщенные координаты и обобщенные скорости, равна
T = 
Вычисляем производные от кинетической энергии системы:
¾по q1 = s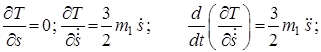 
¾ по q2 = j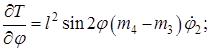 
Для нахождения обобщенных сил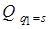 
и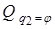 
, соответствующих обобщенным координатам, воспользуемся выражением виртуальной работы сил (2.27), а именно:
В нашем случае:
(2.27)
Эта формула позволяет вычислять обобщенные силы последовательно, учитывая, что обобщенные координаты, а значит, и их вариации независимы между собой. Поэтому системе можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются.
В нашем случае, сначала найдем виртуальную работу:
¾ 
, при 
(2.43)
где 
а выражение в квадратных скобках в уравнении виртуальной работы (2.43 перед вариацией 
есть обобщенная сила:
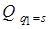
(2.44
Найдем виртуальную работу:
¾ 
, при 
(2.45
где 
Выражение в квадратных скобках в уравнении виртуальной работы (2.45) перед вариацией 
есть обобщенная сила:
= 
.
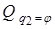(2.46)
Подставляя значения производных от кинетической энергии и выражения для обобщенных сил 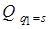(2.44) и 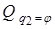(2.46) в уравнения (2.42), получаем дифференциальные уравнения движения системы
1) по q1 = s ¾ 
2) по q2 = j ¾ 
=
=
Поиск по сайту: