Туннельный эффект. Гармонический осциллятор

Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 5.4) для одномерного (по оси х) движения частицы.

Рис. 5.4

Для потенциального барьера прямоугольной формы высоты U и ширины l можно записать:

При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером при E > U, либо отразится от него (E < U) и будет двигаться в обратную сторону, т.е. она не может проникнуть через барьер.

Для микрочастиц же, даже при E < U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E > U имеется также отличная от нуля вероятность, что частица окажется в области x > l, т.е. проникнет сквозь барьер. Такой вывод следует непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при данных условиях задачи.

Уравнение Шредингера для состояний каждой из выделенных областей имеет вид:

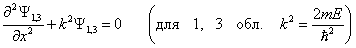	,	(5.4.1)
	.	(5.4.2)

Общее решение этих дифференциальных уравнений:

(5.4.3)

В данном случае, согласно (5.4.2), 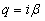– мнимое число, где

Можно показать, что A 1 = 1, B 3 = 0, тогда, учитывая значение q,получим решение уравнения Шредингера для трех областей в следующем виде:

(5.4.4)

В области 2 функция (5.4.4) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени не мнимые, а действительные.

Качественный анализ функций Ψ1(x), Ψ2(x), Ψ3(x) показан на рис. 5.4. Из рисунка следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой.

Таким образом, квантовая механика приводит к принципиально новому квантовому явлению – туннельному эффекту, в результате которого микрообъект может пройти через барьер.

Коэффициент прозрачности для барьера прямоугольной формы .

Для барьера произвольной формы .

Прохождение частицы сквозь барьер можно пояснить соотношением неопределенностей. Неопределенность импульса на отрезке Δ x = l составляет Связанная с этим разбросом кинетическая энергия 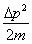может оказаться достаточной для того, чтобы полная энергия оказалась больше потенциальной и частица может пройти через барьер.

С классической точки зрения прохождение частицы сквозь потенциальный барьер при E < U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является с пецифическим квантовым эффектом.

Строгое квантово-механическое решение задачи о гармоническом осцилляторе приводит еще к одному существенному отличию от классического рассмотрения. Оказывается, что можно обнаружить частицу за пределами дозволенной области (, ) (рис. 5.5), т.е. за точками 0 и l (рис. 5.1).

Рис. 5.5

Это означает, что частица может прибывать там, где ее полная энергия меньше потенциальной энергии. Это оказывается возможным вследствие туннельного эффекта.

Основы теории туннельных переходов заложены работами советских ученых Л.И. Мандельштама и М.А. Леонтовича в 1928 г. Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например α-распад, протекание термоядерных реакций).

Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы .

Потенциальная энергия частицы

	,	(5.3.1)
		(5.3.2)

где .

Гармонический осциллятор в квантовой механике описывается уравнением Шредингера:

.

(5.3.3)

Значения Ψ-функции мы находить не будем. Нас интересуют значения полной энергии осциллятора:

,

(5.3.4)

где n = 0, 1, 2…

Рис. 5.3

не зависит от n, в отличие от прямоугольной потенциальной ямы, рассмотренной нами в п. 5.2.

Минимальная энергия называется нулевой энергией, т.е. при колебания атомов К в кристаллической решетке не прекращаются.

В квантовой механике вычисляется вероятность различных переходов квантовой системы из одного состояния в другое. Для гармонического осциллятора возможны лишь переходы между соседними уровнями.

Условия, накладываемые на изменения квантовых чисел при переходах системы из одного состояния в другое, называются правилами отбора. Для гармонического осциллятора правило выражено формулой:

.

Из (5.3.4) вытекает, что энергия квантового осциллятора изменяется только порциями, т.е. квантуется. Причем, как и в прямоугольной яме, энергия ограничена снизу минимальным значением

– энергия нулевых колебаний (прямое следствие соотношения неопределенностей). Это означает, что частица не может находиться на дне потенциальной ямы.

Плотность вероятности нахождения частицы 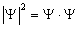изображена на рис. 5.2. Как и в случае прямоугольной потенциальной ямы, при n = 2 в середине ямы частица находиться не может. Это совершенно непонятно с классической точки зрения. Квантуется не только энергия, но и координата частицы.

Поиск по сайту: