Экстремум функции

При значении аргумента функция имеет максимум если в некоторой окрестности точки (возможно весьма малой) выполнено неравенство

Аналогично, при значении аргумента функция имеет минимум если в некоторой окрестности точки (возможно весьма малой) имеет место неравенство

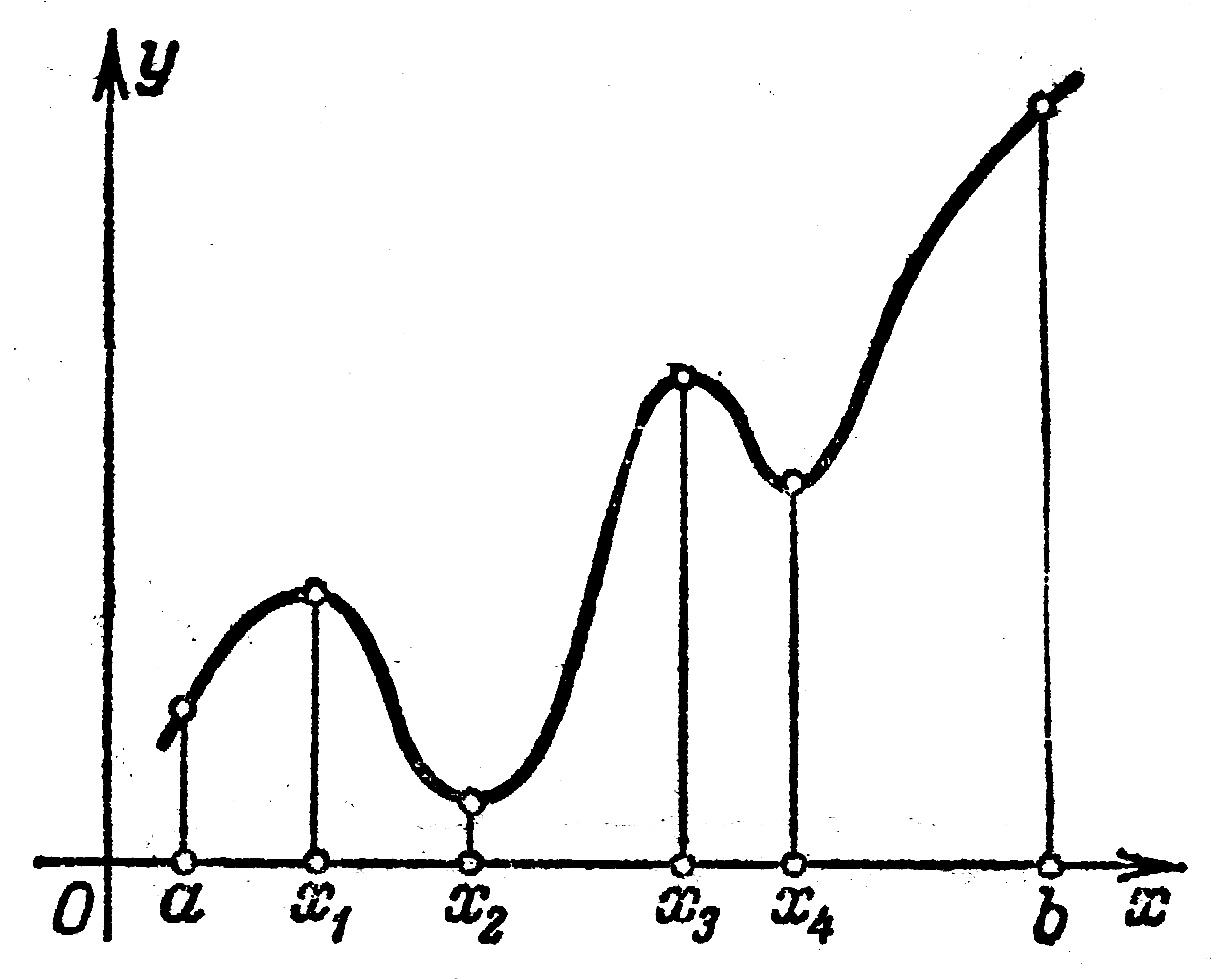Максимум или минимум функции называется экстремумом функции (или экстремальным значением функции). А те значения аргумента, при которых достигаются экстремумы функции, называются точками экстремума функции (соответственно: точками максимума или точками минимума функции). Из определения следует, что экстремум функции, вообще говоря, имеет локальный характер - это наибольшее или наименьшее значение функции по сравнению с близлежащими значениями ее. Минимум функции может быть больше максимума - подобно тому, как впадина в горах может иметь бóльшую отметку над уровнем моря, чем небольшая вершина. На рисунке при и - максимумы, при и - минимумы. Минимум при больше максимума при Из определения максимума и минимума следует: 1) Функция, определенная на отрезке, может достигать максимума и минимума только при значениях заключенных внутри рассматриваемого отрезка. 2) Максимум и минимум функции могут быть, а могут и не быть наибольшим и наименьшим значениями функции на рассматриваемом отрезке. На рисунке наибольшее значение функция принимает в точке 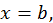а наименьшее в точке

Поиск по сайту: