Через элементарные функции

Мы уже отмечали, что всякая функция 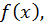непрерывная на интервале имеет на этом интервале первообразную. Однако, не всякая первообразная, даже тогда, когда она существует, выражается в конечном виде через элементарные функции.

Таковы, например, первообразные, выраженные интегралами:

Во всех подобных случаях первообразная представляет собой, очевидно, некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций. Эти новые функции стали называть специальными функциями. Такова, например, функция Лапласа 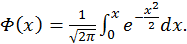Она встретится в теории вероятностей, которая будет изучаться в третьем семестре. Для многих специальных функций составлены таблицы значений при различных значениях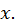

Определенный интеграл

Лекция 15.

Определенный интеграл – одно из основных понятий современной математики. К этому понятию приводят, например, задачи о площади криволинейной трапеции и о вычислении длины пути по заданной скорости.

Поиск по сайту: