 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Числовые ряды
Пусть задана бесконечная последовательность чисел 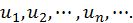
Выражение 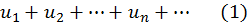
называется числовым рядом (или просто рядом). При этом числа  называются членами ряда.
называются членами ряда.
Сумма конечного числа  первых членов ряда называется
первых членов ряда называется  й частичной суммой ряда:
й частичной суммой ряда: 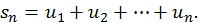
Рассмотрим частичные суммы:
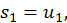

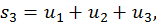

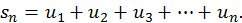
Если существует конечный предел  последовательности
последовательности 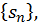 т.е.
т.е.  то его называют суммой ряда
то его называют суммой ряда  и говорят, что ряд сходится.
и говорят, что ряд сходится.
Если  не существует
не существует  например,
например,  при
при  то говорят, что ряд
то говорят, что ряд  расходится и суммы не имеет.
расходится и суммы не имеет.
Пример. 
Это ряд, составленный из членов геометрической прогрессии с первым членом  и знаменателем
и знаменателем 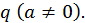
Сумма  первых членов геометрической прогрессии равна
первых членов геометрической прогрессии равна  при
при 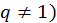
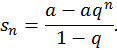
1) Если  то
то  при
при  и, следовательно,
и, следовательно,
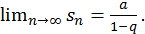
Значит в этом случае ряд  сходится и его сумма
сходится и его сумма 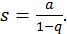
2) Если 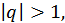 то
то  при
при  и тогда
и тогда  не существует. Таким образом, в этом случае ряд
не существует. Таким образом, в этом случае ряд  расходится.
расходится.
3) Если  то ряд
то ряд  имеет вид:
имеет вид: 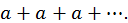
 т.е. ряд расходится.
т.е. ряд расходится.
4) Если  то ряд
то ряд  имеет вид:
имеет вид: 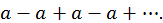
В этом случае  при
при  четном,
четном,  при
при  нечетном.
нечетном.
Следовательно,  предела не имеет,
предела не имеет,  ряд расходится.
ряд расходится.
Поиск по сайту: