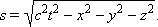|
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Преобразования Лоренца и следствия из них
(относительность одновременности, относительность пространственных и временных промежутков).
Классические преобразования Галилея несовместимы с постулатами СТО и, следовательно, должны быть заменены. Эти новые преобразования должны установить связь между координатами (x, y, z) и моментом времени t события, наблюдаемого в системе отсчета K, и координатами (x', y', z') и моментом времени t' этого же события, наблюдаемого в системе отсчета K'.
Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K' движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид:
|
Из преобразований Лоренца вытекает целый ряд следствий. В частности, из них следует релятивистский эффект замедления времени и лоренцево сокращение длины. Пусть, например, в некоторой точке x' системы K' происходит процесс длительностью τ0 = t' 2 – t' 1 (собственное время), где t' 1 и t' 2 – показания часов в системе K' в начале и конце процесса. Длительность τ этого процесса в системе K будет равна
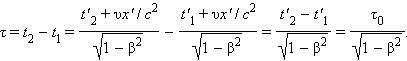
|
Аналогичным образом, можно показать, что из преобразований Лоренца вытекает релятивистское сокращение длины. Одним из важнейших следствий из преобразований Лоренца является вывод об относительности одновременности. Пусть, например, в двух разных точках системы отсчета K' (x' 1 ≠ x' 2) одновременно с точки зрения наблюдателя в K' (t' 1 = t' 2 = t') происходят два события. Согласно преобразованиям Лоренца, наблюдатель в системе K будет иметь
 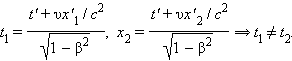
|
Следовательно, в системе K эти события, оставаясь пространственно разобщенными, оказываются неодновременными. Более того, знак разности t 2 – t 1 определяется знаком выражения υ(x' 2 – x' 1), поэтому в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому. Этот вывод СТО не относится к событиям, связанным причинно-следственными связями, когда одно из событий является физическим следствием другого. Можно показать, что в СТО не нарушается принцип причинности, и порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.
Относительность одновременности пространственно-разобщенных событий можно проиллюстрировать на следующем примере.
Пусть в системе отсчета K' вдоль оси x' неподвижно расположен длинный жесткий стержень. В центре стержня находится импульсная лампа B, а на его концах установлены двое синхронизованных часов (рис. 4.4.1(a)), система K' движется вдоль оси x системы K со скоростью υ. В некоторый момент времени лампа посылает короткие световые импульсы в направлении концов стержня. В силу равноправия обоих направлений свет в системе K' дойдет до концов стержня одновременно, и часы, закрепленные на концах стержня, покажут одно и то же время t'. Относительно системы K концы стержня движутся со скоростью υ так, что один конец движется навстречу световому импульсу, а другой конец свету приходится догонять. Так как скорости распространения световых импульсов в обоих направлениях одинаковы и равны c, то, с точки зрения наблюдателя в системе K, свет раньше дойдет до левого конца стержня, чем до правого (рис. 4.4.1(b)).

|
| Рисунок 4.4.1. Относительность одновременности. Световой импульс достигает концов твердого стержня одновременно в системе отсчета K' (a) и не одновременно в системе отсчета K (b) |
Преобразования Лоренца выражают относительный характер промежутков времени и расстояний. Однако, в СТО наряду с утверждением относительного характера пространства и времени важную роль играет установление инвариантных физических величин, которые не изменяются при переходе от одной системы отсчета к другой. Одной из таких величин является скорость света в вакууме c, которая в СТО приобретает абсолютный характер. Другой важной инвариантной величиной, отражающей абсолютный характер пространственно-временных связей, является интервал между событиями.
Пространственно-временной интервал определяется в СТО следующим соотношением:
|
где t 12 – промежуток времени между событиями в некоторой системе отсчета, а l 12 – расстояние между точками, в которых происходят рассматриваемые события, в той же системе отсчета. В частном случае, когда одно из событий происходит в начале координат (x 1 = y 1 = z 1 = 0) системы отсчета в момент времени t 1 = 0, а второе – в точке с координатами x, y, z в момент времени t, пространственно-временной интервал между этими событиями записывается в виде
|
С помощью преобразований Лоренца можно доказать, что пространственно-временной интервал между двумя событиями не изменяется при переходе из одной инерциальной системы в другую. Инвариантность интервала означает, что, несмотря на относительность расстояний и промежутков времени, протекание физических процессов носит объективный характер и не зависит от системы отсчета.
Если одно из событий представляет собой вспышку света в начале координат системы отсчета при t = 0, а второе – приход светового фронта в точку с координатами x, y, z в момент времени t (рис. 4.1.3), то
| x 2 + y 2 + z 2 = c 2 t 2, |
и, следовательно, интервал для этой пары событий s = 0. В другой системе отсчета координаты и время второго события будут другими, но и в этой системе пространственно-временной интервал s' окажется равным нулю, так как
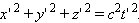
|
Для любых двух событий, связанных между собой световым сигналом, интервал равен нулю.
Из преобразований Лоренца для координат и времени можно получить релятивистский закон сложения скоростей. Пусть, например, в системе отсчета K' вдоль оси x' движется частица со скоростью  Составляющие скорости частицы u'x и u'z равны нулю. Скорость этой частицы в системе K будет равна
Составляющие скорости частицы u'x и u'z равны нулю. Скорость этой частицы в системе K будет равна 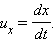
С помощью операции дифференцирования из формул преобразований Лоренца можно найти:
|
Эти соотношения выражают релятивистский закон сложения скоростей для случая, когда частица движется параллельно относительной скорости  систем отсчета K и K'.
систем отсчета K и K'.
При υ << c релятивистские формулы переходят в формулы классической механики:
| ux = u'x + υ, uy = 0, uz = 0. |
Если в системе K' вдоль оси x' со скоростью u'x = c распространяется световой импульс, то для скорости ux импульса в системе K получим

|
Таким образом, в системе отсчета K световой импульс также распространяется вдоль оси x со скоростью c, что согласуется с постулатом об инвариантности скорости света.
Поиск по сайту:
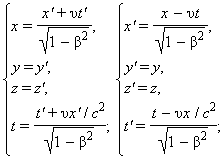 β = υ / c.
β = υ / c.