АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Энергия механических колебаний

Читайте также:
  1. V2: Работа и энергия
  2. V2: Энергия волны
  3. Абсолютно упругий и неупругий удар тел. Внутренняя энергия. Общефизический закон сохранения энергии
  4. Амплитуда, период, частота, фаза колебаний.
  5. В схеме, состоящей из конденсатора и катушки, происходят свободные электромагнитные колебания. Энергия конденсатора в произвольный момент времени t определяется выражением
  6. Внутренняя энергия идеального газа
  7. Внутренняя энергия идеального газа. Работа газа при изобарном расширении. Применение первого начала термодинамики к изопроцессам. Понятие о втором начале термодинамики.
  8. Внутренняя энергия реального газа
  9. Внутренняя энергия реального газа. Эффект Джоуля - Томсона
  10. Внутренняя энергия тела и способы её изменения. Изменение внутренней энергии тела при нагревании. Первое начало термодинамики. Обратимые и необратимые процессы.
  11. Внутренняя энергия. Количество теплоты. Работа в термодинамике
  12. Вопрос 29 Энергия электростатического поля

1. Наибольшая высота подъема математического маятника в процессе колебаний равна двум см. Какова его наибольшая скорость?

Краткая теория:

Для механических колебаний справедлив закон сохранения энергии. В любой момент времени сумма потенциальной и кинетической энергии колеблющегося тела остается постоянной и равной этой сумме в любой другой момент времени. В процессе колебаний происходит превращение потенциальной энергии к кинетическую и обратно. В крайних точках отклонения (амплитудное значение) вся энергия маятника √ потенциальная энергия. При прохождении положения равновесия √ вся энергия кинетическая, скорость маятника максимальна.

Формулы для решения:

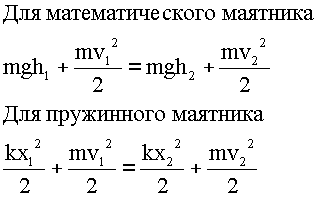
Алгоритм решения типовой задачи:

1. Кратко записываем условие, изображаем его графически.
2. Записываем закон сохранения энергии для математического или пружинного маятника и другие необходимые формулы колебательного движения. Определяем, какие величины надо найти из других механических соотношений, записываем их.
3. Решаем полученные уравнения в общем виде.
4. Подставляем данные, вычисляем. Перед подстановкой переводим все данные в единую систему.
5. Записываем ответ.

Примеры решения:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)