Законы распределения Максвелла и Больцмана

В п. 2.3 мы получили выражение для распределения молекул по скоростям (распределение Максвелла):

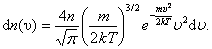
Из этого выражения легко найти распределение молекул газа по значениям кинетической энергии K. Для этого перейдём от переменной υ к переменной :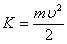

где d n(K) – число молекул, имеющих кинетическую энергию поступательного движения, заключённую в интервале от K до K +d K. Отсюда получим функцию распределения молекул по энергиям теплового движения:

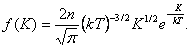
(2.6.1)

Средняя кинетическая энергия молекулы идеального газа:

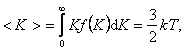
то есть получаем результат, совпадающий с прежним результатом, полученным в п. 1.3.
Итак, закон Максвелла даёт распределение частиц по значениям кинетической энергии, а закон Больцмана – распределение частиц по значениям потенциальной энергии. Оба распределения можно объединить в единый закон Максвелла – Больцмана:

.

(2.6.2)

Здесь n₀ – число молекул в единице объёма в той точке, где U = 0, E = U+K – полная энергия.
В последнем выражении, потенциальная и кинетическая энергии, а следовательно и полная энергия Е, могут принимать непрерывный ряд значений. Если же энергия частицы может принимать лишь дискретный ряд значений Е₁, Е₂ …, (как это имеет место, например, для внутренней энергии атома), то в этом случае распределение Больцмана имеет вид:

,

(2.6.3)

где N_i – число частиц, находящихся в состоянии с энергией E_i, а A> – коэффициент пропорциональности, который должен удовлетворять условию

где N – полное число частиц в рассматриваемой системе.
Тогда окончательное выражение распределения Максвелла – Больцмана для случая дискретных значений энергий будет иметь вид:

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 |

Поиск по сайту:

---