 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Давление под изогнутой поверхностью жидкости
Давление под изогнутой поверхностью жидкости До сих пор мы считали поверхностную плёнку жидкости плоской. Теперь представим,
что она изогнута. 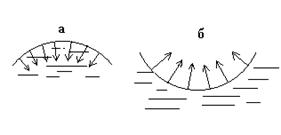 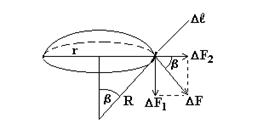 Так как плёнка стремится сократиться, как растянутая резина, ясно, что в случае а)
плёнка оказывает положительное добавочное давление на жидкость,
а в случае б) – отрицательное добавочное давление. Найдём величину этого
добавочного давления. Пусть мы имеем часть выпуклой поверхности жидкости в виде части сферы. Тогда на
каждый элемент ∆ℓ действует сила по касательной к поверхности ∆F = α ∆ℓ.
Разложим силу на составляющие, тогда ∆F1 = ∆F Sin β ∆F2 = ∆F Cos β Сумма всех сил Σ ∆F2 = 0, а сумма всех сил ∆F1 равна: F = Σ ∆F1 = Σ ∆F Sin β = Σ α ∆ℓ (r / R) = α (r / R) Σ ∆l = α 2 π r2 / R Эта сила прижимает сегмент по площади π r2, значит ∆p = F / (π r2) = α 2π r2 / (π r2 R) = 2α / R Вот эту формулу мы и хотели получить. Совершенно ясно,
что для вогнутой поверхности будет ∆p = – 2α / R В общем случае, когда, например, поверхность имеет двоякую кривизну
(седлообразная поверхность) можно написать общую формулу: ∆p = α (1 / R1 + 1 / R2)  Эта формула называется формулой Лапласа. Нужно учитывать только,
что в этом случае R1 > 0 R2 < 0 Из формулы Лапласа тогда вытекают, как частные случаи, формулы для
выпуклой (∆p = 2α / R) и вогнутой (∆p = – 2α / R) поверхностей.
|
Поиск по сайту: