Электромагнитный контур

Рассмотрим колебательный контур, состоящий из конденсатора емкостью C и катушки индуктивностью L (рис. 1.6).

Рис. 1.6. Электромагнитный колебательный контур: 1 - t=0; 2 - t=Т/4; 3 - t=Т/2; 4 - t=3Т/4; 5 - t=Т

Сопротивлением катушки и проводов пренебрегаем. Пусть в цепи идет ток I, заряжающий конденсатор:

Так как внешняя ЭДС к контуру не приложена, то ЭДС самоиндукции

равна напряжению Q/C на конденсаторе.
Имеем два уравнения:

(1.15)

Подставляя первое уравнение во второе, получаем уравнение для изменения заряда на конденсаторе:

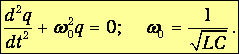
(1.16)

Вместо использованной подстановки выражения тока через заряд можно продифференцировать второе из уравнений (1.15) и выразить производную от заряда через ток. В результате получим аналогичное уравнение для изменения тока в цепи:

(1.17)

с тем же выражением для w₀, что и в (1.16).

Поиск по сайту: