|
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Частица в трехмерной потенциальной яме
Это обобщение предыдущей задачи. Частица может двигаться в кубическом объеме с длиной ребра l. Нетрудно убедиться, что общее решение для волновой функции представимо в виде произведения одномерных волновых функций, полученных в предыдущей задаче:

| (4.26) |
Такая волновая функция соответствует очевидному факту, что движения вдоль трех осей не зависят друг от друга, и каждое описывается прежними одномерными волновыми функциями. Энергия, как легко догадаться, будет равна сумме энергий движения по осям х, у, z
| (4.27) |
Состояние системы теперь определяется тремя квантовыми числами п1, п2 и п3, принимающими, как и прежде; целые значения. Здесь мы впервые сталкиваемся с важным понятием вырождения энергетических уровней, то есть с ситуацией, когда разные состояния системы имеют одинаковую энергию. В самом деле, минимальная энергия системы достигается при минимальных значениях всех квантовых чисел, то есть при п1=п2=п3=1. Эта энергия равна
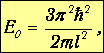
и ей соответствует одна волновая функция y111. Говорят, что основное состояние не вырождено (невырожденность состояния с минимальной энергией - общее правило). Первое возбужденное состояние получается, когда одно из квантовых чисел равно 2, а остальные по-прежнему равны единице; энергия его
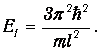
Но такую энергию имеют теперь три состояния с волновыми функциями y112, y121 и y211 (квантовое число 2 можно выбрать тремя способами), поэтому говорят, что кратность вырождения первого возбужденного уровня равна трем (g=3). Естественно, в другой системе может быть совершенно иная кратность вырождения (или отсутствие такового). Последующие состояния частицы в трехмерной потенциальной яме с бесконечными стенками также вырождены. Ясно, что вырождение уровней связано с симметрией системы, с равноправием всех осей. Если бы размеры ямы были разными (l1, l2, l3) то всем трем направлениям, то для энергии мы бы получили вместо (4.27) выражение
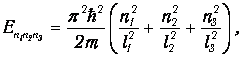
и вырождение могло бы иметь место лишь при определенных соотношениях между длиной, шириной и высотой потенциального ящика.
Поиск по сайту: