Характеристики электрического тока

Все заряженные тела взаимодействуют друг с другом посредством электрических сил, которые для неподвижных частиц описываются законом Кулона. При относительном движении заряженных частиц сила взаимодействия изменяется. Следовательно, движущиеся частицы создают поле, отличное от электростатического, такое поле называется магнитным. Если заряженные частицы движутся хаотически, то суммарное магнитное поле оказывается равным нулю. Поэтому при описании движении заряженных частиц наибольший интерес представляет усредненное направленное движение, приводящее к переносу электрического заряда.

В настоящее время широко известно, что электрические заряды имеют дискретную структуру, то есть носителями зарядов являются элементарные частицы – электроны, протоны и т.д. Однако в большинстве практически значимых случаев эта дискретность зарядов не проявляется, поэтому модель сплошной электрически заряженной среды хорошо описывает явления, связанные с движением заряженных частиц, то есть с электрическим током.

В электростатике мы ввели понятие объемной плотности электрического заряда ρ, как усредненной характеристики распределения дискретных точечных зарядов. В рамках этой же модели можно говорить о движении зарядов как о движении некоторой сплошной среды и использовать математический аппарат, рассмотренный нами при описании движения жидкости, то есть ввести понятия скорости движения «электрической жидкости в данной точке», векторного поля скоростей, линиях тока и т.д. Однако нас интересует не столько движение самой «электрической жидкости», сколько электрический заряд переносимый ею.

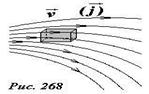
Рассмотрим некоторую пространственную область, в которой движутся электрические заряды («электрическая жидкость»), на рисунке изображены линии тока этого движения. Выделим в этой области малую площадку площадью Δ S перпендикулярную линиям тока (рис. 268). Пусть скорость движения заряда в пределах площадки равна υ ⃗. За промежуток времени Δ t через площадку пройдет заряд, заключенный в объеме параллелепипеда длиной υ Δ t, опирающийся на выбранную площадку (рис. 269).

Величина этого заряда равна Δ q = ρυ Δ t Δ S. Чтобы определить «точечную» характеристику переноса заряда разделим величину заряда, прошедшего через площадку, на площадь площадки и рассматриваемый промежуток времени. Полученная таким образом характеристика называется плотностью электрического тока

j =Δ q Δ t Δ S = ρυ. (1)

Имеет смысл считать данную характеристику векторной, направление которой совпадает с направлением скорости движения зарядов

j ⃗ = ρυ ⃗. (2)

Таким образом, плотностью электрического тока называется векторная физическая величина, модуль которой равен количеству электрического заряда, протекающего в единицу времени через площадку единичной площади, расположенную перпендикулярно направлению движения заряда, а направление совпадает с направлением переноса электрического заряда.

Для того чтобы плотность тока была определена «в каждой точке», рассмотренную площадку следует сделать бесконечно малой.

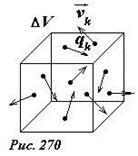
Рассмотрим определение плотности электрического тока с точки зрения дискретного описания. Выделим в объеме движения дискретных зарядов небольшую часть объемом Δ V, содержащую достаточно много заряженных частиц (рис. 270). Пронумеруем все заряженные частицы, находящиеся в этом объеме; обозначим величины зарядов этих частиц q _k, а их скорости υ ⃗ k (k = 1,2,3…N). Построим векторную сумму J ⃗ =∑ kqkυ ⃗ k. Если движение заряженных частиц является хаотическим, то есть скорости частиц равновероятно направлены во все стороны, то данная сумма будет приблизительно равна нулю, если же в движении заряженных частиц присутствует преимущественное направление, то построенная величина будет указывать направление переноса заряда и характеризовать количество этого заряда. Чтобы построенная таким образом характеристика была точечной, необходимо разделить ее на величину выделенного объема и устремить последний к нулю

j ⃗ =∑ kqkυ ⃗ k Δ V. (3)

Покажем теперь, что построенная таким образом величина совпадает с определенной нами выше плотностью тока. Для простоты будем считать, что все заряженные частицы одинаковы q _k = q (например, электроны в металле). Определим среднюю арифметическую скорость движения частиц < υ ⃗ >=∑ kυ ⃗ kN, из которого следует, что ∑ kυ ⃗ k = N < υ ⃗ >. С учетом этого выражения, формула преобразуется к виду

j ⃗ =∑ kqkυ ⃗ k Δ V = q ∑ kυ ⃗ k Δ V = qN < υ ⃗ >Δ V = qn < υ ⃗ >, (4)

где обозначено n = N Δ V - число заряженных частиц в единице объема, то есть их концентрация. Произведение же концентрации частиц на их электрический заряд равно электрическому заряду, заключенному в единице объема, то есть объемной плотности заряда qn = ρ. Таким образом, формула (4) совпадает с формулой (2), если скорость движения «электрической жидкости» отождествить со средней скоростью движения заряженных частиц.

В качестве наглядной модели движения заряженных частиц можно представить движения облака комаров, каждый из которых движется хаотически в пределах облака, а под действием ветерка это облако целиком смещается в некотором направлении.

Если в переносе заряда участвует несколько типов заряженных частиц, то можно определить плотность тока каждого типа части, а суммарную плотность тока, как сумму плотностей токов всех типов частиц. Так в растворе поваренной соли могут двигаться положительно заряженные ионы натрия Na ⁺ и отрицательно заряженные ионы хлора Cl ^-. В этом случае вектор плотности тока выражается суммой

j ⃗ = j ⃗ ++ j ⃗ −= q + n +< υ ⃗ +>+ q − n −< υ ⃗ −>, (5)

где j ⃗ +, j ⃗ − - плотности токов, q ⁺, q ^- - заряды, n ⁺, n ^- - концентрации, < υ ⃗ +>,< υ ⃗ −> - средние скорости ионов натрия и хлора, соответственно.

Заметим, что согласно данному определению вектор плотности тока совпадает со скоростью движения положительных зарядов, при движении отрицательных зарядов вектор плотности тока противоположен вектору их скорости. Иными словами за положительное направление движения электрического тока принимается направление движения положительных зарядов.

В большинстве применений электрический ток проходит по металлам, в которых носителями тока являются отрицательно заряженные электроны, поэтому, как ни странно, чаще всего направление тока противоположно направлению движения реальных частиц электронов. Такая несуразность также является следствием исторической традиции – направление электрического тока было определено еще в начале XIX века, когда о природе носителей тока не имели ни малейшего представления.

Таким образом, мы определили векторную характеристику переноса заряда – плотность тока. Этот вектор определен в каждой точке пространства, поэтому с математически движение зарядов описывается векторным полем j ⃗ (x, y, z).

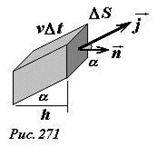
Рассмотрим физический смысл потока ^[1] данного векторного поля. Для этого мысленно выделим малую площадку площадью Δ S, в пределах которой вектор плотности тока j ⃗ можно считать постоянным и направленным под углом α к вектору нормали площадки n ⃗ (рис. 271). Если скорость направленного движения заряда равна υ, то за время Δ t через площадку пройдет заряд, содержащийся в наклонном параллелепипеде, длина стороны которого равна υ Δ t. Величина этого заряда равна произведению объемной плотности заряда на объем параллелепипеда Δ q = ρ Δ Sh = ρ Δ Sυ Δ t cos α. Следовательно, в единицу времени через площадку протекает электрический заряд равный

I =Δ q Δ t = ρ Δ Sυ cos α = j Δ S cos α = j ⃗ ⋅ n ⃗ Δ S =Φ j. (6)

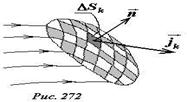
Как следует из полученного соотношения, данная величина равна потоку вектора плотности тока j ⃗ через площадку Δ S. Если требуется найти количество заряда протекающего через некоторую поверхность (рис. 272), в пределах которой вектор плотности тока изменяется, то следует поступать традиционным образом: разбить поверхность на малые площадки, найти по формуле (6) поток через каждую площадку, после чего просуммировать эти потоки

Φ j =∑ k ΔΦ jk =∑ kj ⃗ k ⋅ n ⃗ k Δ Sk.

Поток вектора плотности тока играет важную роль в изучении электрического тока, поэтому получил «персональное» наименование – сила электрического тока.

Поиск по сайту: