АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Свойства векторного произведения

Читайте также:
  1. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  2. V2: Электрические и магнитные свойства вещества
  3. Акустические свойства голоса
  4. Акустические свойства строительных материалов
  5. Алгебраические свойства векторного произведения
  6. Алгоритм вычисления произведения
  7. АЛГОРИТМ И ЕГО СВОЙСТВА
  8. Аллювиальные отложения и их свойства
  9. Антигенные свойства антител.
  10. Антитела. Строение, свойства, продукция.
  11. АТМОСФЕРА И ЕЕ СВОЙСТВА
  12. Атрибуты и свойства материи

1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa) (см. рис. 19).

Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а, b, а хb и a, b, bxa противоположной ориентации). Стало быть axb = -(bxa).

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. l(а хb) = (lа) х b = а х (lb).

Пусть l>0. Вектор l(ахb) перпендикулярен векторам а и b. Вектор (lа)хb также перпендикулярен векторам а и b (векторы а, lа лежат в одной плоскости). Значит, векторы l(ахb) и (lа)хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:

Поэтому l(a хb)= lахb. Аналогично доказывается при l<0.

3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b <=>ахb =0.

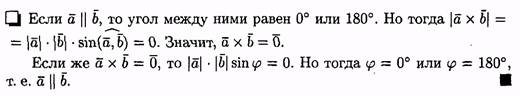
В частности, i *i =j *j =k *k =0.

4. Векторное произведение обладает распределительным свойством:

(a+b) хс= ахс+b хс.

7) Определение.

Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.

Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.

Смешанное произведение векторов a = {ax; ay; az}, b = {bx; by; bz} и c = {cx; cy; cz} в декартовой системе координат можно вычислить, используя следующую формулу:

a · [b × c] = ax ay az
bx by bz
cx cy cz

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)