Замечание. При нахождении предела функции , которая является непрерывной, можно переходить к пределу под знаком функции

При нахождении предела функции , которая является непрерывной, можно переходить к пределу под знаком функции, то есть

Пример

Задание. Вычислить предел

Решение.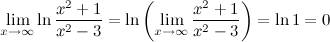

Ответ.

Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

функция определена в точке и ее окрестности;

существует конечный предел функции в точке ;

это предел равен значению функции в точке , т.е. называется точкой разрыва функции.

Пример

Функция не определена в точке , а значит, эта точка является точкой разрыва указанной функции.

29) Свойства функций, непрерывных на отрезке

Теорема. Пусть функция непрерывна на отрезке . Тогда справедливы следующие утверждения:

(1) она достигает на этом отрезке своего наибольшего и своего наименьшего значения, т.е. такие, что для ;

(2) функция достигает на отрезке любое промежуточное значение, т.е. если m – наименьшее, а M – наибольшее значение на этом отрезке и – любое число, удовлетворяющее неравенствам: , то такая, что ;

(3) если функция на концах отрезка принимает значения разных знаков, т.е. , то внутри отрезка найдется такая точка 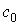(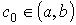), что .

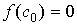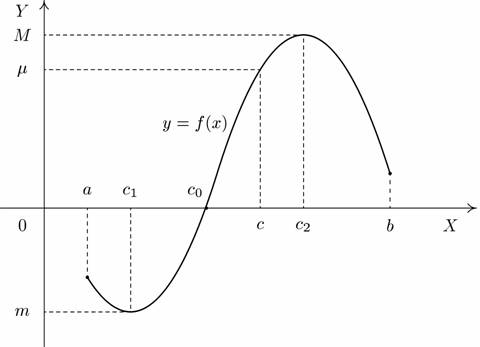
Иллюстрации к теореме приведены на следующем рисунке.

30) Задача 1 (о скорости движения). По прямой, на которой заданы начало отсчета, единица измерения (метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой s=s(t), где t — время (в секундах), s(t) — положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с).

Решение. Предположим, что в момент времени t тело находилось в точке M.

Дадим аргументу t приращение Δt и рассмотрим ситуацию в момент времени t+Δt. Координата материальной точки станет другой, тело в этот момент будет находиться в точке P:OP=s(t+Δt).

Значит, за Δt секунд тело переместилось из точки M в точку P. Имеем: MP=OP−OM=s(t+Δt)−s(t). Полученную разность мы назвали в приращением функции: s(t+Δt)−s(t)=Δs. Итак, MP=Δs(м). Нетрудно найти среднюю скорость vср движения тела за промежуток времени [t;t+Δt]: vср=ΔsΔt (м/с).

А что такое скорость v(t) в момент времени t (ее называют мгновенной скоростью)? Можно сказать так: это средняя скорость движения за промежуток времени [t;t+Δt] при условии, что Δt выбирается все меньше и меньше; точнее: при условии, что Δt→0. Это значит, что v(t)=limΔt→0vср.

Итак,

v=limΔt→0ΔsΔt

31) Приращением функции f в точке x0, соответствующим приращению ∆х называется разность f(x0 + ∆х) – f(x0). Приращение функции обозначается следующим образом ∆f. Таким образом получаем, по определению:

· ∆f= f(x0 +∆x) – f(x0).

Иногда, ∆f еще называют приращением зависимой переменной и для обозначения используют ∆у, если функция была, к примеру, у=f(x).

Поиск по сайту: