ВОПРОС 11

Отдельный интерес представляют системы, в которых на тела действуют потенциальные силы. Для таких сил вводится понятие потенциальной энергии, изменение которой в случае одной материальной точки по определению удовлетворяет соотношению:

Где и — значения потенциальной энергии точки в начальном и конечном состояниях соответственно, а 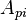— работа потенциальной силы, совершаемая при перемещении точки из начального состояния в конечное.

Изменение потенциальной энергии системы получается в результате суммирования изменений энергий всех тел системы:

Если все внутренние и внешние силы, действующие на тела системы, потенциальны, то

Подставляя полученное выражение в уравнение теоремы о кинетической энергии, получим:

или, что то же самое

Иначе говоря, получается, что для полной механической энергии системы выполняется

Таким образом, можно сделать вывод: если на тела системы действуют только потенциальные силы, то полная механическая энергия системы сохраняется.

Данное утверждение и составляет содержание закона сохранения механической энергии, являющегося следствием теоремы о кинетической энергии и одновременно частным случаем общего физического закона сохранения энергии

Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение^[1].

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

Начав двигаться, тело имеет тенденцию продолжать движение. Первый закон механики Ньютона гласит: если тело движется, то при отсутствии внешних воздействий оно так и будет двигаться дальше прямолинейно и равномерно до тех пор, пока оно не подвергнется воздействию внешней силы. Эту тенденцию называют линейным импульсом. С ней часто сталкиваемся в повседневной жизни. Бильярдный шар катится по столу с той скоростью, которая придана ему кием, копье летит с той скоростью, с которой его метнули.

Физики определяют линейный импульс тела p как его массу m, умноженную на его скорость v:

p = m v

Буквы p и v выделены полужирным шрифтом, чтобы показать, что эти величины характеризуются не только абсолютным значением, но и направлением. Так, применительно к скорости, мы не просто говорим, что машина движется со скоростью 40 км/ч, а что она движется со скоростью 40 км/ч, например, на север. Величина, которая кроме абсолютного значения имеет направление, называется вектором.

Понятно, что, согласно первому закону Ньютона, количество движения отдельно взятого тела в отсутствии внешних сил сохраняется. Закон же сохранения импульса гласит, что при соблюдении этого условия сохраняется векторная сумма импульсов всех тел, входящих в замкнутую механическую систему. В таком представлении система из двух бильярдных шаров массой m, пущенных друг навстречу другу с одинаковыми скоростями v, будет иметь нулевой момент импульса, хотя каждый из шаров по отдельности и обладает импульсом m v. Однако импульсы шаров взаимно погасятся вследствие их векторной природы (поскольку их скорости противоположно направлены).

Вообще, любая величина, характеризующая систему и не изменяющаяся в результате взаимодействия внутри нее, называется консервативной, и для нее имеется свой закон сохранения. В частности, в механических системах, помимо закона сохранения импульса действует еще и закон сохранения момента импульса или количества вращения — величины, которая описывает количество движения тел вокруг собственной оси и по изогнутым траекториям.

Что же происходит при прямолинейном соударении двух бильярдных шаров на встречных курсах? Происходит сразу несколько явлений. Во-первых, в момент столкновения шары слегка деформируются и часть их кинетической энергии переходит в тепловую. Во-вторых, мы знаем, что совокупный импульс системы из двух шаров не изменяется и остается равным нулю. Значит, видя, что один шар откатывается после лобового столкновения в обратном направлении с определенной скоростью, мы можем с уверенностью сказать, что второй шар в данный момент времени катится в обратном направлении с ровно той же скоростью.

Второй закон механики Ньютона, кстати, можно легко интерпретировать и как формулу, согласно которой скорость изменения импульса равна силе, приложенной к замкнутой системе. Таким образом, чтобы изменить импульс системы, требуется внешняя сила. В молекулярно-кинетической теории, например, это наглядно просматривается: давление объясняется импульсами ударов молекул о стенки сосуда, содержащего газ. Поскольку молекулы газа упруго отскакивают в обратном направлении, их импульсы меняются на противоположные, а значит, стенка оказывает силовое воздействие на ударяющиеся об нее молекулы. Но это означает, что и молекулы, в силу третьего закона Ньютона, оказывают силовое воздействие на стенку, которое и воспринимается нами как давление.

Вращающееся вокруг своей оси тело при отсутствии тормозящих вращение сил так и будет продолжать вращаться. Физики привычно объясняют этот феномен тем, что такое вращающееся тело обладает неким количеством движения, выражающимся в форме углового момента количества движения или, кратко, момента импульса или момента вращения. Момент импульса вращающегося тела прямо пропорционален скорости вращения тела, его массе и линейной протяженности. Чем выше любая из этих величин, тем выше момент импульса. Если теперь допустить, что тело вращается не вокруг собственного центра массы, а вокруг некоего центра вращения, удаленного от него, оно всё равно будет обладать вращательным моментом импульса. В математическом представлении момент импульса L тела, вращающегося с угловой скоростью ω, равен L = Iω, где величина I, называемая моментом инерции, является аналогом инерционной массы в законе сохранения линейного импульса, и зависит она как от массы тела, так и от его конфигурации — то есть, от распределения массы внутри тела. В целом, чем дальше от оси вращения удалена основная масса тела, тем выше момент инерции.

Сохраняющейся или консервативной принято называть величину, которая не изменяется в результате рассматриваемого взаимодействия. В рамках закона сохранения момента импульса консервативной величиной как раз и является угловой момент вращения массы — он не изменяется в отсутствие приложенного момента силы или крутящего момента — проекции вектора силы на плоскость вращения, перпендикулярно радиусу вращения, помноженной на рычаг (расстояние до оси вращения). Самый расхожий пример закона сохранения момента импульса — фигуристка, выполняющая фигуру вращения с ускорением. Спортсменка входит во вращение достаточно медленно, широко раскинув руки и ноги, а затем, по мере того, как она собирает массу своего тела всё ближе к оси вращения, прижимая конечности всё ближе к туловищу, скорость вращения многократно возрастает вследствие уменьшения момента инерции при сохранении момента вращения. Тут мы и убеждаемся наглядно, что чем меньше момент инерции I, тем выше угловая скорость ω и, как следствие, короче период вращения, обратно пропорциональный ей.

Следует отметить, однако, что не любая приложенная извне сила сказывается на моменте вращения. Предположим, вы поставили свой велосипед «на попа» (колесами вверх) и сильно раскрутили одно из его колес. Понятно, что, приложив тормозящую силу трения к любой окружности колеса (нажав на ручной тормоз, приложив руку к резине или вращающимся спицам), вы, тем самым, снизите угловую скорость его вращения. Однако, сколько бы вы ни старались, вы не остановите вращения колеса, пытаясь воздействовать на ось вращения. Иными словами, для изменения момента вращения необходима не просто сила, а момент силы — то есть, сила, приложенная по направлению, отличному от направления оси вращения, и на некотором удалении от нее. Поэтому закон сохранения момента вращения можно сформулировать и несколько иначе: момент вращения тела изменяется только в присутствии момента силы, направленной на его изменение.

И тут возникает важное дополнительное замечание. До сих пор мы говорили об изменении момента вращения в плане ускорения или замедления вращения, как такового, но при этом тело продолжало вращаться всё в той же плоскости, и ось вращения не изменяла своей ориентации в пространстве. Теперь предположим, что момент силы приложен в плоскости, которая отличается от плоскости, в которой вращается тело. Такое воздействие неизбежно приведет к изменению направления оси вращения. В отсутствие же внешних воздействий закон сохранения момента импульса подразумевает, что направление оси вращения остается неизменным. Этот принцип широко используется в так называемых гироскопических навигационных приборах. В их основе лежит массивное, быстро вращающееся колесо — гироскоп, — которое не изменяет своей ориентации в пространстве, благодаря чему прибор стабильно указывает заданное направление, вне зависимости от угла поворота субмарины, самолета или спутника, на котором он установлен. С технической точки зрения гироскоп представляет собой массивный диск на осевых подшипниках низкого трения, раскрученный с очень большой скоростью. Идеальный гироскоп — это диск бесконечной массы, вращающийся с бесконечной скоростью в идеальном вакууме. В таком случае закон сохранения момента импульса подскажет нам, что направление оси такого идеального гироскопа не отклонится от исходной ни на одну угловую секунду, и он вечно будет указывать нам на изначально заданную точку. Искусственные спутники Земли, как правило, оснащаются несколькими независимыми гироскопами, вращающимися в разных плоскостях, и бортовая электроника, сопоставляя данные нескольких гироскопических компасов и усредняя поправки на возможные отклонения их показаний, безошибочно определяет координаты и ориентацию спутника в околоземном пространстве.

Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на систему, которая совершает колебания. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида

где ω₀ — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω₀t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А.

Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий название период колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.

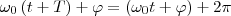
Откуда

Величина, обратная периоду колебаний,

т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем

Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса.

Найдем первую и вторую производные по времени от величины s, совершающей гармонические колебания:

Из выражения непосредственно вытекает дифференциальное уравнение гармонических колебаний

(где s = A cos(ω₀t+φ)). Решением данного дифференциального уравнения является выражение (1).

Гармонические колебания графически изображаются методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, которая выбрана на оси х, под углом φ, который равен начальной фазе колебания, откладывается вектор А, у которого модуль равен амплитуде А рассматриваемого колебания (рис. 2). Если данный вектор привести во вращение с угловой скоростью ω₀, которая равна циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения от –А до +А, а колеблющаяся величина будет изменяться со временем по закону s = Acos(ω₀t+φ). Значит, гармоническое колебание можно представить как проекцию на некоторую выбранную произвольным образом ось вектора амплитуды А, который отложен из произвольной точки оси под углом φ, равным начальной фазе, и вращающегося с угловой скоростью ω₀ вокруг этой точки.

В физике часто используется другой метод, отличающийся от метода вращающегося вектора амплитуды лишь по форме. В данном методе колеблющуюся величину представляют комплексным числом. Используя формулу Эйлера, для комплексных чисел

где - мнимая единица. Значит уравнение гармонического колебания (1) можно представить в комплексной форме:

Вещественная часть формулы (8)

есть гармоническое колебание. Обозначение Re вещественной части условимся опускать и (8) записывать в форме

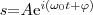
В теории колебаний уславливаются, что колеблющаяся величина s равна вещественной части комплексного выражения, стоящего в этом равенстве справа.

Гармоническим осциллятором называется система, которая совершает колебания, описываемые выражением вида d²s/dt² + ω₀²s = 0

где две точки сверху означают двукратное дифференцирование по времени. Колебания гармонического осциллятора есть важный пример периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. В качестве примеров гармонического осциллятора могут быть пружинный, физический и математический маятники, колебательный контур (для токов и напряжений настолько малых, что можно было бы элементы контура считать линейными).

1. Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид

Или

Из формулы (1) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω₀t+φ) с циклической частотой

И периодом

Формула (3) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна

2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела (рис. 1).

Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы

где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, F_τ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления F_τ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение (4) запишем как

или

Принимая

получим уравнение

идентичное с (1), решение которого (1) найдем и запишем как:

Из формулы (6) вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω₀ и периодом

3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника

где l — длина маятника.

Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то, подставив (8) в (7), найдем выражение для периода малых колебаний математического маятника

Сопоставляя формулы (7) и (9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Значит, приведенная длина физического маятника — это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного физического маятника.

Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.

где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ

или

Перепишем это уравнение в следующем виде:

Где представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда

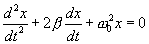
Будем искать решение уравнения (7.19) в виде

где U - некоторая функция от t.

Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим

Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение тогда С вещественным ω решением этого уравнения, как мы знаем, является функция

Таким образом, в случае малого сопротивления среды , решением уравнения (7.19) будет функция

График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,

Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.

Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда

Откуда

Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда

Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз.

Вынужденными колебаниями называются колебания, возни­кающие в системе при участии внешней силы, изменяющейся по периодическому закону.

Предположим, что на материальную точку, кроме квазиупру­гой силы и силы трения, действует внешняя вынуждающая сила

где F₀ — амплитуда, — круговая частота колебаний вынуждаю­щей силы. Составим дифференциальное уравнение (второй закон Ньютона):

Или

Решение дифференциального уравнения (5.41) является сум­мой двух слагаемых. Одно из них, соответствующее уравнению затухающих колебаний (5.20), играет роль только при установле­нии колебаний (см. рис. 5.6). Со временем им можно пренебречь. Другое слагаемое описывает смещение материальной точки в ус­тановившихся вынужденных колебаниях

Где

Как видно из (5.42), установившееся вынужденное колебание, происходящее под воздействием гармонически изменяющейся вы­нуждающей силы, тоже является гармоническим. Частота вынуж­денного колебания равна частоте вынуждающей силы. Вынужден­ные колебания, график которых представлен на рис. 5.17, сдвину­ты по фазе относительно вынуждающей силы.

Амплитуда вынужденного колебания (5.43) прямо пропорци­ональна амплитуде вынуждающей силы и имеет сложную зави­симость от коэффициента затухания среды и круговых частот соб­ственного и вынужденного колебаний. Если w₀ и b для системы заданы, то амплитуда вынужденных колебаний имеет максималь­ное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Само явление — достижение максимальной амплитуды вынужденных колебаний для за­данных w₀ и b — называют резонансом.

Резонансную круговую частоту можно найти из условия мини­мума знаменателя в (5.43):

Подставив (5.45) в (5.43), находим амплитуду при резонансе:

Механический резонанс может быть как полезным, так и вред­ным явлением. Вредное действие резонанса связано главным об­разом с разрушением, которое он может вызвать. Так, в технике, учитывая разные вибрации, необходимо предусматривать воз­можное возникновение резонансных условий, в противном случае могут быть разрушения и катастрофы. Тела обычно имеют не­сколько собственных частот колебаний и соответственно несколь­ко резонансных частот.

Если бы коэффициент затухания внутренних органов человека был невелик, то резонансные явления, возникшие в этих органах под воздействием внешних вибраций или звуковых волн, могли бы привести к трагическим последствиям: разрыву органов, по­вреждению связок и т. п. Однако такие явления при умеренных внешних воздействиях практически не наблюдаются, так как ко­эффициент затухания биологических систем достаточно велик. Тем не менее резонансные явления при действии внешних меха­нических колебаний происходят во внутренних органах. В этом, видимо, одна из причин отрицательного воздействия инфразвуковых колебаний и вибраций на организм человека

Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде

где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как

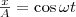
и заменяя во втором уравнении на и на , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей: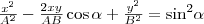

Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.

Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес:

1) α = mπ (m=0, ±1, ±2,...). В этом случае эллипс становится отрезком прямой

где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой, которое совершается вдоль прямой (3), составляющей с осью х угол. В этом случае имеем дело с линейно поляризованными колебаниями;

2) α = (2m+1)(π/2) (m=0, ± 1, ±2,...). В этом случае уравнение станет иметь вид

Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно-поляризованными колебаниями или колебаниями, поляризованными по кругу.

Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ).

Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко применяемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.

1. Механические волны.