Зонная пластинка

- экран (в простейшем случае - стеклянная пластинка), состоящий из системы чередующихся прозрачных и непрозрачных концентрич. колец, ширина к-рых подобрана так, чтобы расстояние от краёв соседних прозрачного и непрозрачного колец (рис.) до точки наблюдения F, называемой фокусом 3. п., изменялось на длину полуволны; NF-MF=l/2, где l - длина волны. Т. о., 3. п. делит падающую на неё волну на кольцевые Френеля зоны. Фазы волн, излучаемых соответствующими точками N и М каждых двух соседних зон, противоположны. Если между точечным источником и точкой наблюдения расположить 3. п. с k прозрачными кольцами, соответствующими нечётным зонам

Френеля (чётные зоны - непрозрачные), то действие всех выделенных (прозрачных) зон сложится и амплитуда колебаний в точке наблюдения возрастёт в 2k раз; то же получится, если прозрачными будут чётные зоны, но фаза суммарной волны будет иметь противоположный знак. Если на стеклянную пластинку вместо непрозрачного слоя нанести прозрачный слой, вызывающий сдвиг фазы на l/2, то интенсивность света в точке наблюдения возрастёт в 4k раз. Т. о., 3. п. увеличивает освещённость в точке наблюдения подобно собирательной (положительной) линзе.

7. Дифракция плоских волн на щели.

При наблюдении дифракции Фраунгофера источник и экран «находятся на бесконечно больших расстояниях» от щели (дифракционной решетки или другого препятствия), т.е. на щель падает волна с плоским волновым фронтом, и после прохождения щели мы анализируем интерференцию волн от вторичных источников в бесконечно удаленной точке. Если 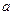- расстояние до источника, - расстояние до экрана, 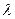- длина волны света, 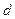- ширина щели, то должно выполняться соотношение 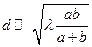(1). Экспериментально световая волна формируется лазером (при необходимости пучок расширяют) или точечным источником, расположенным в фокусе собирающей линзы. За щелью располагают экран на большом расстоянии от нее или сразу за щелью располагают собирающую линзу, в фокальной плоскости которой наблюдают дифракционную картину на экране. Возможны и другие способы размещения источника и экрана, для которых не выполняется соотношение (1), но они выходят за рамки данной лекции.

В рассматриваемом случае дифракции на решетке, вклад от каждой из ее щелей мал и составляет 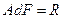. С учетом сдвига фаз он может быть представлен алгебраически в виде 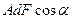– действительной части комплексного числа 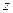или геометрически в виде проекции радиус вектора комплексного числа 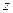на горизонтальную ось. Соответствующая сумма вкладов от щелей решетки может быть представлена как

8. Рисунок 3 — Дифракция Фраунгофера на щели.

Рассмотрим дифракцию на щели. Разобьем фронт плоской световой волны, прошедшей через щель, на 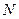полосок одинаковой ширины – вторичные источники света. Тогда вклад от каждого из них будет одинаков по модулю, а сдвиг фаз между соседними вторичными источниками, будет определяться шириной полоски и углом между нормалью.

Выберем две точк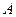и и 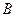волнового фронта волны, падающей на щель. Тогда для анализа интенсивности плоской световой волны, распространяющейся после дифракции на щели 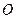под углом относительно нормали к плоскости объекта, разность фаз между ними будет равна (треугольник ABC – прямоугольный). Таким образом, если всю щель равномерно разбить на участки одинаковой площади, то вектора будут иметь одинаковую длину, а сдвиг фаз между каждыми двумя последовательными векторами будет составлять , где - ширина щели, 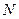- число участков, 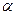- суммарный сдвиг фаз между первым и последним векторами (соответствуют краям щели). Получаем фигуру, которая в пределе 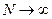переходит в дугу окружности.

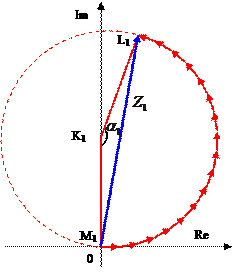
Рисунок 4 — Векторные диаграммы для расчета интенсивности картины дифракции
Фраунгофера на щели.

9.

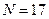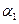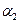На рисунках для случая представлены векторные интерпретации образования векторов суммы и для двух суммарных сдвигов фаз и , соответствующих различным точкам наблюдения на экране. Из геометрических соображений находим радиусы окружностей 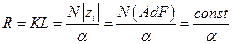, и значение модуля вектора суммы 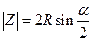. Поскольку все вектора «вращаются» с одинаковой угловой скоростью 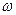, то наибольшая интенсивность в каждой точке наблюдения будет определяться модулем вектора суммы. Интенсивность света может быть вычислена по формуле:

, где 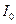- интенсивность света в точке, в которой сдвиг фаз равен нулю. При падении света по нормали сдвиг фаз равен нулю при распространении света по нормал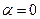и при . Если излучение на объект (щель) падает под углом относительно нормали, то сдвиг фаз будет определяться формулой 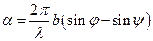. Нулевой сдвиг фаз будет в направлении свободного распространения света 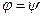, как если бы дифракции на объекте (щели) не было.

Точки минимума интенсивности определяются из равенства 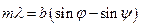, 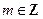. Большая часть энергии сосредоточена в диапазоне углов .

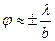Поиск по сайту: