Понятие спектрального разложения сигнала

Для теории, а также для техники формирования и обработки сигналов важное значение имеет разложение сигнала, заданного в виде функции, по различным ортогональным системам функций.

Как было впервые показано французским физиком Фурье, любую произвольную функцию u(x) даже обладающую конечным числом разрывов можно представить в виде бесконечной суммы синусных и косинусных членов

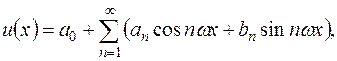(1.1)

Раздел математики, устанавливающий соотношение между функцией u(x) (или её отсчётами) и коэффициентами и , стали называть гармоническим анализом, вследствие функции с синусными и косинусными членами этой суммы, названной впоследствии рядом Фурье [14].

Любая система ортогональных функций может быть применена для разложения в ряды, которые соответствуют рядам Фурье. Например, в теории связи часто используется разложение в ряды по функциям Уолша, Лагерра, Бесселя. Для многих систем функций имеется также преобразование, подобное преобразования Фурье.

Поэтому для представления сигналов и характеристик линий и цепей вместо частной системы синусоидальных и косинусоидальных функций вполне применима обобщённая полная система ортогональных функций.

Спектральное разложение в этом случае представляет собой сумму обобщённого ряда Фурье:

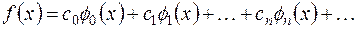(1.2)

где коэффициенты ряда определяются по формулам:

(1.3)

а функции представляют собой систему ортогональных функций на отрезке [a,b].

Обобщённый ряд Фурье обладает следующим важным свойством: при заданной системе функций и при фиксированном числе слагаемых ряда (1.2) он обеспечивает наилучшую аппроксимацию (в смысле минимума среднеквадратичной ошибки) данной функции .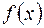

Выбор наиболее ортогональной системы функций зависит от цели, преследуемой при разложении сложной функции в ряд. Среди разнообразных задач, требующих разложения сложного сигнала, можно выделить прежде всего два важных направления:

1) точное разложение на простейшие ортогональные функции;

2) аппроксимация сигналов, процессов и характеристик, когда требуется свести к минимуму число членов ряда (при заданной допустимой погрешности).

При первой постановке задачи наибольшее распространение получила ортогональная система основных тригонометрических функция – синусов и косинусов. Особая роль этих функций объясняется ряжом причин: 1) гармоническое колебание является простейшей функцией, определённой при всех значениях x, и не поддаётся дальнейшему разложению в спектр; 2) гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении колебания через любую линейную систему (с постоянными параметрами). Изменяется лишь амплитуда и фаза колебания. Далее, разложение сложного сигнала по синусам и косинусам позволяет использовать символический метод, разработанный для анализа передачи гармонических колебаний через линейные цепи.

По этим, а также и другим причинам, гармонический анализ получил широкое распространение во всех отраслях современной науки и техники.

При второй постановке задачи - «удобной» аппроксимации функций – применяются разнообразные ортогональные системы функций, например:

1) полиномы Чебышева, Эрмита, Лагерра, Лежандра и другие;

2) функции Уолша, Хаара и другие;

3) функции, составляющие базис преобразования Карунена-Лоэва.

Каждый вид ортогональных систем имеет свою область применения. В зависимости от класса сигнала ортогональные системы специальных функций могут быть подобраны таким образом, чтобы требуемая точность представления обеспечивалась при минимуме членов ряда. При выборе системы функций также учитывается математическая сложность выполнения преобразований, возможность достаточно простой генерации функций, входящих в базис, возможность построения фильтрующих устройств в данном ортогональном базисе и множество других факторов.

В последующих пунктах рассмотрим подробнее разложение по обозначенным трём классам ортогональных систем.

Поиск по сайту: