Использование вынужденных переходов для усиления электромаrнитноrо поля

То обстоятельство, что вынужденное излучение возбужденных микрочастиц при переходах с верхнего энергетического уровня на нижний когерентно (совпадает по частоте, фазе, по­ляризации и направлению распространения) с вынуждающим, наталкивает на мысль о возможности использования вынужденных переходов для усиления электромагнитного поля. Чтобы оценить возможность такого усиления, рассмотрим обмен энергии между полем и веществом. Будем предполагать, что вещество имеет два энергетических уровня Е₁ и Е₂ с населенностями N₁ и N₂, а частота внешнего поля равна частоте квантового перехода ν₂₁. При объемной плотности энергии u_ν число вынужденных переходов в единицу времени в единице объема с выделением энергии n₂₁ = Bu_νN₂, а выделяемая при этих переходах энергия в единице объема в единицу времени, т.е. мощность

. (3.23)

Аналогично число вынужденных переходов с поглощением энергии и поглощаемая от внешнего поля мощность в единице объема соответственно

(3.24)

(3.25)

Изменение мощности электромагнитного поля

(3.26)

Назовем эту величину мощностью взаимодействия.

Если Р > 0, т.е. выделяемая мощность превышает поглощаемую, то в системе происхо­дит увеличение энергии поля или усиление электромагнитного поля. При Р < О преобладает поглощение энергии, и энергия внешнего поля убывает.

Таким образом, условием усиления (Р > 0) будет N₂ - N₁ > 0 или N_2/N₁ > 1.

В состоянии термодинамического равновесия населенность верхнего уровня меньше, чем нижнего (N₂ < N₁) в соответствии с законом Больцмана. Поэтому вещество в этом со­стоянии поглощает энергию внешнего поля (Р < 0), так как число квантовых переходов пl2 снизу вверх (1 → 2) с поглощением энергии больше числа квантовых переходов сверху вниз (2 → l) с выделением энергии.

Соотношение N₂ > N₁ является обратным (инверсным) по отношению к состоянию тер­модинамического равновесия, когда N₂ < N₁. Поэтому состояние, при котором N₂ > N₁, т.е. возможно усиление, называют состоянием с инверсией населенностей уровней.

Закон Больцмана, справедливый для термодинамического равновесия, можно записать так:

. (3.27)

Величину Т_п называют температурой перехода. Формально при состоянии с инверсией населенностей эта температура отрицательна (Т_п < 0).

Среда, в которой имеется состояние с инверсией населенностей, называется также актив­ной средой, так как в ней возможно усиление электромагнитного поля.

В состоянии термодинамического равновесия N₁ > N₂, поэтому при воздействии элек­тромагнитного поля число вынужденных переходов снизу вверх (l → 2) больше числа вы­нужденных переходов сверху вниз (2 → 1): населенность нижнего уровня убывает, а верх­него - растет. При достаточно большой объемной плотности энергии поля u_v может про­изойти выравнивание населенностей уровней (N₁ и N₂), когда числа вынужденных перехо­дов 1 → 2 и 2 →1 равны, т.е. наступает динамическое равновесие. Явление выравнивания населенностей уровней называют насыщением перехода. Таким образом, при воздействии электромагнитного поля на двухуровневую систему можно добиться насыщения перехода, но не инверсии населенностей.

Населенности уровней при любом значении объемной плотности энергии поля находят­ся из решения скоростных (кинетических) уравнений. Для двухуровневой системы скорости изменения населенностей уровней:

(3.28)

где N- полное число частиц.

Поясним процедуру составления уравнений. Населенность уровня 1 в единицу времени убывает вследствие вынужденных переходов 1 → 2 на величину N₁Bu_ν, а из-за безызлуча­тельных переходов 1 → 2 - на величину N₁E₁₂. Одновременно происходит рост населенно­сти N₁, вследствие переходов 2 → 1 на величину N₂Bu_ν (вынужденные переходы), N₁ A₂₁ (спонтанные переходы) и N₂E₂₁ (безызлучательные переходы). Первые два слагаемых учи­тывают увеличение N₂ в результате вынужденных и безызлучательных переходов 1 → 2, а остальные определяют убывание N₂ вследствие вынужденных, спонтанных и безызлуча­тельных переходов 2 → 1.

Очевидно, что для двухуровневой системы при сохранении полного числа частиц dN₁/dt= -dN₂Idt.

В стационарном состоянии dN₁/dt = dN₂/dt = 0, поэтому можно написать систему двух уравнений

(3.29)

Решая эту систему уравнений, можно найти стационарные величины N₁ и N₂, а затем их разность и отношение:

(3.30)

(3.31)

(3.32)

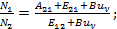(3.33)

(3.34)

Показаны зависимости N₁ и N₂ от объемной плотности энергии П_ν для случая, когда система до воздействия электромагнитного поля находилась в термодинамическом равнове­сии с населенностями N_1b и N_2b, определяемыми законом Больцмана. Из этого следует, что при малых значениях П_ν населенность нижнего уровня N₁ убывает, а верхнего N₂ растет по линейному закону. При очень больших значениях плотности энергии (П_ν →∞) N₁ и N₂ стре­мятся к среднему значению N/2 = (N_1b + N_2b)/2, соответствующему насыщению переходов.

При отсутствии поля (П_ν = 0) населенности уровней равны и 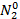, причем .

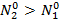С ростом П_ν N₂ убывает, а N₁ растет от значений и 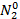по линейному закону, но при больших П_ν асимптотически они приближаются к среднему значению N/2, соответствующему насыщению перехода.

Разность населенностей уровней (N₂ – N₁) определяет мощность взаимодействия:

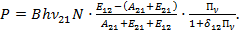(3.35)

Эта формула позволяет найти зависимость мощности взаимодействия от объемной плотности энергии 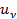электромагнитного поля, взаимодействующего с веществом. Зависи­мость Р(П_v) определяется отношением . При увеличении u_ν мощность сначала (при ) линейно растет, а затем стремится к предельному значению Р_прсд, которое определяется путем раскрытия неопределенности при П_ν→∞, т.е. в состоянии насыщения перехода

(3.36)

Используя соотношение и учитывая, что обычно вероятность релаксационных перехо­дов много больше вероятности спонтанных, выражению можно придать более простой и наглядный вид

(3.37)

где - время релаксации.

В состоянии насыщения при П_ν→∞ (N₁ = N₂), когда мощность, выделяемая при вынуж­денных переходах 2 → 1, равна мощности, поглощаемой при вынужденных переходах 1→ 2, от электромагнитного поля отбирается мощность Р_прсд. Эта мощность необходима для под­держания равенства населенностей уровней, которое постоянно стремится нарушаться из-за наличия спонтанных и безызлучательныx переходов с вероятностями А₂₁, Е₂₁ и E₁₂- Число этих переходов непосредственно от плотности энергии не зависит и определяется только населенностью уровней. Получаемая от электромагнитного поля энергия рассеивается в ве­ществе, например в кристаллической решетке в виде теплоты.

Поиск по сайту: