 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Интерференция. Опыт Юнга
При наложении в пространстве двух (или нескольких) когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих воли. Это явление называется интерференцией волн. Волны называются когерентными, если разность их фаз остается постоянной во времени. Рассмотрим интерференционную картину, полученную методом Юнга (рис. 8.2).
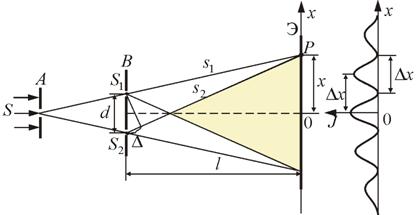
Рис. 8.2
Свет от источника S, прошедший через узкую щель в экране А, падет на экран В с двумя щелями S 1 и S 2, расположенными достаточно близко друг к другу на расстоянии d. Эти щели являются когерентными источниками света. Интерференция наблюдается в области, в которой перекрываются волны от этих источников (поле интерференции). На экране Э мы видим чередование полос с максимумом и минимумом интенсивности света.
максимумы интенсивности будут наблюдаться в случае, если
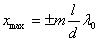 (m = 0, 1, 2, …) (m = 0, 1, 2, …)
|
а минимумы – в случае, если
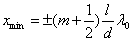
|
Расстояние между двумя соседними максимумами (или минимумами) равно:
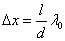 , ,
|
Поиск по сайту: