АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Асимптоты графика функции

Читайте также:
  1. II. Основные задачи и функции
  2. III. Предмет, метод и функции философии.
  3. IV. Конструкция бент-функции
  4. Ms Excel: мастер функций. Логические функции.
  5. V2: ДЕ 29 - Введение в анализ. Предел функции на бесконечности
  6. V2: ДЕ 32 - Дифференциальное исчисление функции одной переменной. Производная
  7. V2: ДЕ 35 - Дифференциальное исчисление функции одной переменной. Производные высший порядков
  8. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  9. V2: Функции исторической науки
  10. VIII. ФУНКЦИИ НАУЧНОГО ИССЛЕДОВАНИЯ
  11. XVIII. ПРОЦЕДУРЫ И ФУНКЦИИ
  12. А) ПЕРЕДАЧА НА РУССКОМ ЯЗЫКЕ ФУНКЦИИ АРТИКЛЯ

● Прямая 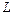называется асимптотой графика функции , если расстояние от некоторой точки , лежащей на графике, до этой прямой 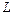стремится к нулю при стремлении хотя бы одной из координат точки к бесконечности.

Существуют два вида асимптот: вертикальные и наклонные.

 

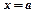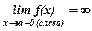● Прямая называется вертикальной асимптотой графика функции , если

 

или 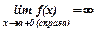. (4.3.1)

Вертикальных асимптоты ищутся среди точек разрыва.

 

Пример 4.3.1. Найти вертикальные асимптоты графиков функций:

1) 2)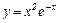

Решение.

1) Вертикальные асимптоты ищутся среди точек разрыва, т. е. в нашем случае рассмотрим .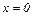

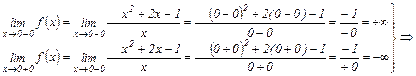
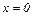– вертикальная асимптота.

2) Очевидно, вертикальных асимптот нет, т. к. нет точек разрыва.

● Прямая 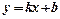называется наклонной асимптотой графика функции , если существуют конечные пределы:

левая наклонная асимптота при правая наклонная асимптота при 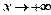(4.3.2)
, , , .

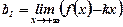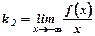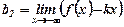Замечание. В некоторых случаях функция асимптотически приближается к одной и той же прямой пр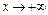и и 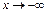, тогда наклонная асимптота будет одна при .

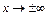● При прямая 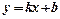примет вид и наклонная асимптота будет горизонтальной.

Пример 4.3.2. Найти наклонные асимптоты графиков функций

1) 2)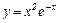

Решение.

1)

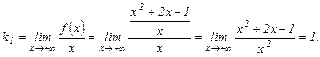
Соответственно,

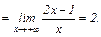
Таким образом, имеется правая (при 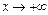) наклонная асимптота 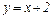. Аналогично можно показать, что эта же прямая является наклонной асимптотой и при .

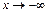Таким образом, при 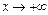так и при 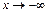функция асимптотически приближается к одной и той же прямой (рис. 4.3.1).

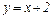Рис. 4.3.1

2)

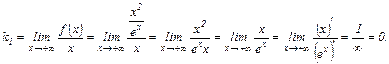
Соответственно,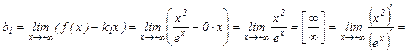

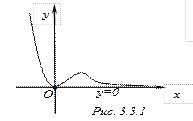
Таким образом, имеется правая (при 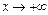), т. к. 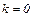горизонтальная асимптота .

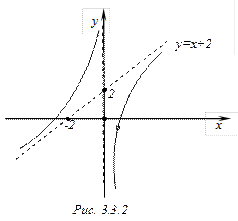
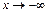Следовательно, при асимптот не будет (рис. 4.3.2).

Рис. 4.3.2

Пример 4.3.3. Найти асимптоты графиков функций

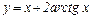
1) 2)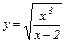

Решение.

1) Очевидно, вертикальных асимптот нет, т. к. нет точек разрыва.

Исследуем поведение функции при 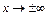, т. е. найдём наклонные (горизонтальные) асимптоты .

;

Соответственно, .

Таким образом, 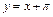– правая наклонная асимптота.

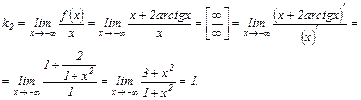
Соответственно,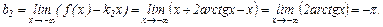

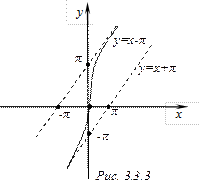
Таким образом, 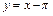– левая наклонная асимптота (рис.4.3.3).

Рис. 4.3.3

2) Функция определена в интервалах .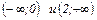

Так как

,

,

то только прямая 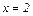является вертикальной асимптотой.

 

Исследуем поведение функции при 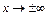, т. е. найдём наклонные (горизонтальные) асимптоты .

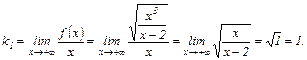
Соответственно,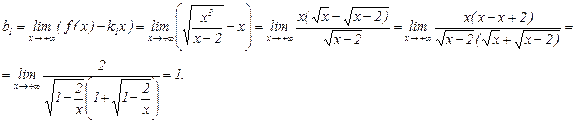

Таким образом, существует правая наклонная асимптота .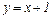

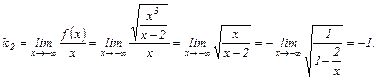
Соответственно,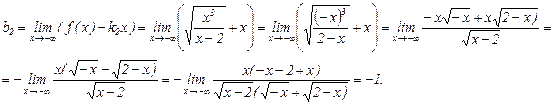

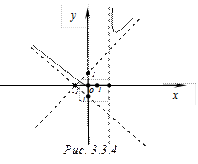
Таким образом, правая наклонная асимптота 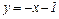(рис. 4.3.4).

Рис. 4.3.4


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.56 сек.)