Формула тонкой линзы

,

где a и b – расстояния от оптического центра линзы соответственно до предмета и изображения;

– относительный показатель преломления ( n и n₁ – соответственно абсолютные показатели преломления линзы и среды, окружающей линзу );

R₁ и R₂ – радиусы кривизны поверхностей линзы.

Подставив в формулу тонкой линзы:

соотношения , R₁=R₂=R (линза имеет одинаковые радиусы кривизны поверхностей) и n₁= 1 (среда, окружающая линзу, – воздух), получим:

Умножим обе части выражения н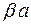а :

, откуда .

Тогда расстояние от предмета до изображения

.

Подставим числовые значения: .

Задача №3 (5.45). Расстояние между двумя щелями в опыте Юнга d = 0,5 мм (λ = 0,6 мкм). Определите расстояние l от щелей до экрана, если ширина ∆ x интерференционных полос равна 1,2 м м.

Дано: Решение:

Рис.

d = 0,5 мм = 5 ^. 10^–4 м

λ = 0,6 мкм = 6 ^. 10^–7 м

∆ x= 1,2 мм = 1,2 ^. 10^–3 м

l –?

В методе Юнга источником света служит ярко освещенная щель S (рис.), от которой световая волна падает на две узкие равноудаленные щели S ₁ и S ₂, параллель­ные щели S,являющиеся когерентными источниками, а интерференционная картина наблюдается на экране (Э), расположенном на некотором расстоянии l от щелей S ₁ и S ₂ (рис.).

Щели S ₁ и S ₂ находятся на расстоянии d друг от друга (рис. 4), причем l >> d.

Интерференция рассматривается в произ­вольной точке А на экране, расположенной на расстоянии x от точки O, симметричной от­носительно щелей и принятой за начало отсчета величины x.

Интенсивность в любой точке А экрана, лежащей на расстоянии х от точки О, определяется оптической разностью хода D = s ₂ – s ₁ .

Согласно рисунку:

; ,

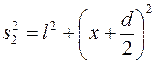откуда

или .

Из условия l >> d следует, что s ₁ + s ₂ » 2 l, тогда

, откуда .

Если оптическая разность хода D равна целому числу длин волн l ₀, т.е.

( = 0, 1, 2,…),

то колебания, возбуждаемые в точке А обеими волнами, будут проис­ходить в

одинаковой фазе и в точке А будет наблюдаться интерференционный максимум (m – порядок интерференционного максимума).

Если же оптическая разность хода D равна полуцелому числу длин волн l ₀, т.е.

( = 0, 1, 2,…),

то колебания, возбуждаемые в точке А обеими волнами, будут происходить в противофазе и в точке А будет наблюдаться интерференционный минимум (m – порядок интерференционного минимума).

Подставляя в соотношение условия наблюдения интерференционных максимумов и минимумов, определим положения максимумов (x_max) и минимумов (x_min) интенсивности на экране в методе Юнга:

( = 0, 1, 2,…),

( = 0, 1, 2,…).

Расстояние между двумя соседними максимумами (или минимумами) D x называется шириной интерференционной полосы и равно:

,

откуда .

Подставим числовые значения: .

Задача №4 (5.68). Точечный источник света(λ = 0,5 мкм) расположен на расстоянии a = 1 м перед диафрагмой с круглым отверстием диаметра d = 2 мм. Определите расстояние b от диафрагмы до точки наблюдения, если отверстие открывает три зоны Френеля.

Дано: Решение:

λ = 0,5 мкм = 5 ^. 10^–7 м

a =1 м

d = 2 мм = 2 ^. 10^–3 м

m = 3

b –?

Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием (рис.). Дифрак­ционную картину наблюдаем на экране Э в точке В, соединяющей S с центром отверстия. Согласно условию задачи, отверстие диафрагмы открывает m зон Френеля, поэтому разбиваем поверхность Ф фронта волны, идущей от источника S (поверхность Ф является сферической поверхностью с центром в точке S) на m сферических сегментов (кольцевых зон) такого размера, чтобы расстояния от краев каждой зоны до точки В отличались на l /2 (рис.). Обозначим радиус внешней границы m -ой зоны через r_m, высотусферическогосегмента, выделяемого внешней границей m -ой зоны – h_m.

Из рисунка 5 следует, что

.

С другой стороны,

.

В полученных выражениях возведем скобки в квадрат:

,

.

Произведем элементарные преобразования

,

.

Учитывая, что и , слагаемым можно пренебречь по сравнению . При не слишком больших m (по условию задачи m = 3) высота сегмента 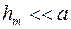и , поэтому слагаемым можно пренебречь по сравнению и .

C учетом этих приближений:

,

.

Отсюда

,

.

или

,

.

После подстановки в формулу, определяющую расстояние b от диафрагмы до точки наблюдения, получим

.

Учитывая, что , найдем .

Подставим числовые значения: .

Задача №5 (5.88). На дифракционную решетку нормально падает монохроматический свет с длиной волны λ = 600 нм. Определите наибольший порядок спектра, полученный с помощью этой решетки, если ее постоянная d = 2 мкм.

Дано: Решение:

λ = 600 нм = 6 ^. 10^–7 м

d = 2 мкм = 2 ^. 10^–6 м

m_max –?

Формула дифракционной решетки: (условие наблюдения максимумов(рис.)):

( = 0, 1, 2, …, m_max),

– постоянная дифракционной решетки;

– длина световой волны;

– угол дифракции,

– номер дифракционных максимумов (порядок спектра),

m_max – наибольший номер дифракционных максимумов (наибольший порядок спектра).

Наибольший порядок спектра m_max найдем, записав формулу дифракционной решетки в виде:

, откуда .

Поскольку наибольший угол дифракции не может быть более (), то и .

Оценим отношение : .

Учитывая, что число m (порядок спектра) должно быть целым, то наибольший порядок спектра m_max,полученный с помощью данной решетки: m_max = 3.

Поиск по сайту: