 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Поверхности второго порядка в пространстве. Исследование поверхностей методом сечений. Цилиндрические и конические поверхности. Поверхности вращения
Литература. [1]§ 74, 75, 76.
Поверхность пространства является алгебраической второго порядка в том и только в том случае, когда в некоторой аффинной системе координат ее уравнение имеет вид:
 Не оговаривая особо, в дальнейшем будем предполагать, что в пространстве дана прямоугольная декартовая система координат.
Не оговаривая особо, в дальнейшем будем предполагать, что в пространстве дана прямоугольная декартовая система координат.
Любую поверхность можно рассматривать как множество линий, полученных при ее пересечении всеми плоскостями, параллельными между собой. Такой способ называется методом сечений. Будем рассматривать множества плоскостей, параллельных плоскостям координат.
Пусть в пространстве даны поверхность р и плоскость p, параллельная координатной плоскости Оху и определенная уравнением  . Обозначим через g¢ - линию пересечения р и p, а через g - проекцию g¢ на координатную плоскость Оху.
. Обозначим через g¢ - линию пересечения р и p, а через g - проекцию g¢ на координатную плоскость Оху.
Определение 1. Кривая g называется линией уровня поверхности р на плоскости Оху, соответствующей значению h.
Аналогично определяются линии уровня поверхности р на координатных плоскостях Oxz и Оуz.
Теорема 1. Пусть уравнение поверхности Р в системе координат  имеет вид
имеет вид  . Тогда уравнение
. Тогда уравнение  представляет собой уравнение ее линии уровня g ¢ на плоскости Оху, соответствующей значению h, в системе координат
представляет собой уравнение ее линии уровня g ¢ на плоскости Оху, соответствующей значению h, в системе координат  .
.
 Доказательство. Возьмем произвольную точку
Доказательство. Возьмем произвольную точку  , принадлежащую g. Покажем, что ее координаты ‑ решение уравнения
, принадлежащую g. Покажем, что ее координаты ‑ решение уравнения  . Так как М лежит на g, то существует точка M¢ кривой g¢ пересечения Р и плоскости
. Так как М лежит на g, то существует точка M¢ кривой g¢ пересечения Р и плоскости  , которая проектируется параллельно оси
, которая проектируется параллельно оси 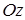 в точку М (рис. 96). M¢ лежит в p и проектируется в точку М, поэтому ее координаты равны:
в точку М (рис. 96). M¢ лежит в p и проектируется в точку М, поэтому ее координаты равны:  . Но точка M¢ лежит на поверхности Р. Ее координаты удовлетворяют уравнению поверхности
. Но точка M¢ лежит на поверхности Р. Ее координаты удовлетворяют уравнению поверхности  . Таким образом, координаты М удовлетворяют уравнению линии g.
. Таким образом, координаты М удовлетворяют уравнению линии g.
Обратно, пусть М - некоторая точка плоскости, координаты х и у которой в системе  удовлетворяют уравнению
удовлетворяют уравнению  . Покажем, что М принадлежит линии уровня g. Рассмотрим точку М¢ плоскости p, которая проектируется параллельно оси
. Покажем, что М принадлежит линии уровня g. Рассмотрим точку М¢ плоскости p, которая проектируется параллельно оси 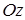 в точку М. Координаты М ¢ равны:
в точку М. Координаты М ¢ равны:  . Так как они удовлетворяют уравнению
. Так как они удовлетворяют уравнению  , то M¢ лежит на поверхности Р. Поэтому M¢ принадлежит пересечению g¢ поверхности Р и плоскости p, a точка М находится на проекции g линии g¢ на плоскость Оху. Теорема доказана.
, то M¢ лежит на поверхности Р. Поэтому M¢ принадлежит пересечению g¢ поверхности Р и плоскости p, a точка М находится на проекции g линии g¢ на плоскость Оху. Теорема доказана.
Аналогично определяются уравнения линий уровня поверхности на координатных плоскостях Oxz и Оуz. Например, уравнение линии уровня поверхности Р:  на плоскости Оуz, соответствующей значению h, т. е. при пересечении плоскостью
на плоскости Оуz, соответствующей значению h, т. е. при пересечении плоскостью  ,в системе координат
,в системе координат 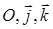 имеет вид:
имеет вид:  . Меняя h, получим систему линий уровня на каждой из координатных плоскостей. Такие системы позволяют судить о форме поверхности. Метод сечений используется на практике. Например, с его помощью на топографических картах изображается рельеф местности, а на морских ‑ рельеф дна.
. Меняя h, получим систему линий уровня на каждой из координатных плоскостей. Такие системы позволяют судить о форме поверхности. Метод сечений используется на практике. Например, с его помощью на топографических картах изображается рельеф местности, а на морских ‑ рельеф дна.
 Перейдем к изучению цилиндрических поверхностей.
Перейдем к изучению цилиндрических поверхностей.
Определение 2. Поверхность называется цилиндрической, если она вместе с каждой своей точкой содержит прямую, параллельную некоторому фиксированному ненулевому вектору.
Прямые цилиндрической поверхности, параллельные указанному вектору, называются ее образующими. Ясно, что любую цилиндрическую поверхность можно определить, выбрав в пространстве кривую g и ненулевой вектор  , а затем построить прямые, параллельные
, а затем построить прямые, параллельные  , проходящие через точки кривой g (рис. 97). Кривая g называется направляющей цилиндрической поверхности. Простейшей цилиндрической поверхностью является плоскость. Ее направляющей может служить ее любая прямая, а образующие могут быть параллельны произвольному вектору этой плоскости, который не параллелен направляющей прямой.
, проходящие через точки кривой g (рис. 97). Кривая g называется направляющей цилиндрической поверхности. Простейшей цилиндрической поверхностью является плоскость. Ее направляющей может служить ее любая прямая, а образующие могут быть параллельны произвольному вектору этой плоскости, который не параллелен направляющей прямой.
Теорема 2. Пусть образующие цилиндрической поверхности параллельны оси аппликат прямоугольной декартовой системы координат  , а ее направляющая принадлежит координатной плоскости Оху и имеет уравнение
, а ее направляющая принадлежит координатной плоскости Оху и имеет уравнение  в системе координат
в системе координат  этой плоскости. Тогда это же уравнение
этой плоскости. Тогда это же уравнение  является уравнением всей поверхности в системе координат
является уравнением всей поверхности в системе координат  пространства.
пространства.
 Доказательство. Выберем произвольную точку
Доказательство. Выберем произвольную точку  , принадлежащую данной цилиндрической поверхности. Проведем через нее образующую l, которая пересечет направляющую g в некоторой точке
, принадлежащую данной цилиндрической поверхности. Проведем через нее образующую l, которая пересечет направляющую g в некоторой точке  (рис. 98). Так как образующая параллельна оси Оz, то у точки
(рис. 98). Так как образующая параллельна оси Оz, то у точки  в системе
в системе  координаты совпадают с первыми двумя координатами точки М:
координаты совпадают с первыми двумя координатами точки М:  . Так как
. Так как  принадлежит g, то ее координаты удовлетворяют уравнению
принадлежит g, то ее координаты удовлетворяют уравнению  . Следовательно, координаты точки М удовлетворяют тому же уравнению.
. Следовательно, координаты точки М удовлетворяют тому же уравнению. 
Обратно, пусть координаты х, у и z некоторой точки М удовлетворяют уравнению  . Покажем, что она лежит на данной цилиндрической поверхности. Проведем через М прямую l, параллельную оси аппликат и обозначим через
. Покажем, что она лежит на данной цилиндрической поверхности. Проведем через М прямую l, параллельную оси аппликат и обозначим через  точку пересечения l с плоскостью Оху. Координаты точки
точку пересечения l с плоскостью Оху. Координаты точки  в системе
в системе  равны:
равны:  . Но по условию х и у удовлетворяют уравнению кривой g:
. Но по условию х и у удовлетворяют уравнению кривой g:  . Поэтому
. Поэтому  лежит на направляющей g, следовательно, l ‑ образующая цилиндрической поверхности. Данная точка М лежит на этой поверхности. Теорема доказана.
лежит на направляющей g, следовательно, l ‑ образующая цилиндрической поверхности. Данная точка М лежит на этой поверхности. Теорема доказана.
 С помощью этой теоремы можно описать все вещественные цилиндрические поверхности второго порядка. Для этого на плоскости Оху в качестве направляющей выберем кривую второго порядка, а образующие этой поверхности будут параллельны оси аппликат.
С помощью этой теоремы можно описать все вещественные цилиндрические поверхности второго порядка. Для этого на плоскости Оху в качестве направляющей выберем кривую второго порядка, а образующие этой поверхности будут параллельны оси аппликат.
1) Эллиптический цилиндр: 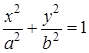 .
.
2) Гиперболический цилиндр:  .
.
3) Параболический цилиндр:  .
.
4) Цилиндрическая поверхность, представляющая собой пару плоскостей, пересекающихся на оси Оz:  .
.
5) Цилиндрическая поверхность, представляющая собой пару параллельных плоскостей:  .
.
6) Цилиндрическая поверхность, представляющая собой пару слившихся параллельных плоскостей:  .
.
На рисунках 99 а) - в) изображены эллиптический, гиперболический и параболический цилиндры.
Рассмотрим свойства вещественной конической поверхности второго порядка.
 Определение 3. Поверхность р называется конической, если для нее можно указать такую точку О, для которой прямая, проходящая через нее и любую другую точку поверхности, целиком принадлежит p.
Определение 3. Поверхность р называется конической, если для нее можно указать такую точку О, для которой прямая, проходящая через нее и любую другую точку поверхности, целиком принадлежит p.
Эти прямые называются образующими конической поверхности. Точка, в которой пересекаются все образующие, называется вершиной. Любую коническую поверхность можно построить следующим образом. Выберем в пространстве некоторую кривую g и зафиксируем точку О. Затем через нее и через каждую точку кривой проведем прямые, образующие конической поверхности. В этом случае кривая g называется направляющей этой поверхности (рис. 100). Докажем следующую теорему.
Теорема 3. Поверхность, заданная уравнением
 , (1)
, (1)
является конической с вершиной в начале координат.
Доказательство. Выберем на этой поверхности произвольную точку  . Ее координаты удовлетворяют уравнению (25.1):
. Ее координаты удовлетворяют уравнению (25.1):  . Если О - начало координат, то координаты вектора
. Если О - начало координат, то координаты вектора  равны
равны  . Поэтому параметрические уравнения прямой
. Поэтому параметрические уравнения прямой  имеют следующий вид:
имеют следующий вид:

Возьмем произвольную точку М этой прямой, соответствующей параметру t, и покажем, что ее координаты  и
и  удовлетворяют уравнению (1). Действительно,
удовлетворяют уравнению (1). Действительно,  . Таким образом, прямая
. Таким образом, прямая  целиком лежит на поверхности. Теорема доказана.
целиком лежит на поверхности. Теорема доказана.

Уравнение (25.1) называется каноническим уравнением вещественной конической поверхности второго порядка. Построим ее линии уровня на координатных плоскостях. Рассмотрим плоскость Оху. Пусть плоскость сечения имеет уравнение  . Тогда уравнение соответствующей линии уровня имеет вид:
. Тогда уравнение соответствующей линии уровня имеет вид: 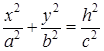 . При
. При  получим:
получим:  . Этому уравнению соответствует начало системы координат, т.е. вершина конуса. Если
. Этому уравнению соответствует начало системы координат, т.е. вершина конуса. Если  , то преобразуем уравнение линии уровня к виду:
, то преобразуем уравнение линии уровня к виду: 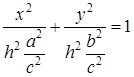 . Полученное уравнение при любом h, отличном от нуля, определяет эллипс, оси симметрии которого совпадают с осями координат. Отношение его полуосей равно
. Полученное уравнение при любом h, отличном от нуля, определяет эллипс, оси симметрии которого совпадают с осями координат. Отношение его полуосей равно  , т.е. не зависит от h. Таким образом, линии уровня на плоскости Оху представляют собой множество подобных между собой эллипсов, имеющих одни и те же оси симметрии, причем с увеличением h полуоси эллипсов бесконечно возрастают (рис. 101, а).
, т.е. не зависит от h. Таким образом, линии уровня на плоскости Оху представляют собой множество подобных между собой эллипсов, имеющих одни и те же оси симметрии, причем с увеличением h полуоси эллипсов бесконечно возрастают (рис. 101, а).
Рассмотрим теперь сечения поверхности плоскостью  , параллельной координатной плоскости Oxz. Линия уровня на плоскости определяется уравнением:
, параллельной координатной плоскости Oxz. Линия уровня на плоскости определяется уравнением:  . Если
. Если  , то линия уровня определяется уравнением
, то линия уровня определяется уравнением  т.е. представляет собой две прямые
т.е. представляет собой две прямые  ‑ образующие конической поверхности. Пусть
‑ образующие конической поверхности. Пусть  . Преобразуем уравнение к виду:
. Преобразуем уравнение к виду:  . В этом случае линией уровня является гипербола, для которой оси координат Оz и Ox служат действительной и мнимой осями симметрии, а отношение действительной полуоси к мнимой постоянно, не зависит от h и равно
. В этом случае линией уровня является гипербола, для которой оси координат Оz и Ox служат действительной и мнимой осями симметрии, а отношение действительной полуоси к мнимой постоянно, не зависит от h и равно  . Поэтому все эти гиперболы имеют одни
. Поэтому все эти гиперболы имеют одни  и те же асимптоты, определяемые уравнениями:
и те же асимптоты, определяемые уравнениями:  , т.е. прямые, которые, в свою очередь, служат линиями уровня конической поверхности при
, т.е. прямые, которые, в свою очередь, служат линиями уровня конической поверхности при  .
.
 Карта линий уровня
Карта линий уровня  приведена на рисунке 101, б. Ясно, что аналогичную карту линий уровня получим при пересечении поверхности плоскостями
приведена на рисунке 101, б. Ясно, что аналогичную карту линий уровня получим при пересечении поверхности плоскостями 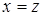 . На рисунке 102 изображена вещественная каноническая поверхность второго порядка, показаны сечения плоскостями, параллельными координатным плоскостям Оху и Oxz.
. На рисунке 102 изображена вещественная каноническая поверхность второго порядка, показаны сечения плоскостями, параллельными координатным плоскостям Оху и Oxz.
Интересно отметить следующий факт. Если пересечь коническую поверхность второго порядка плоскостью, параллельной ее образующей, то в сечении образуется парабола. Это сечение изображено на рисунке 103. Эллипс, гиперболу и параболу часто называют коническими сечениями.
Определение 4. Поверхность р называется поверхностью вращения, если для нее можно указать такую прямую l, что она вместе с каждой своей точкой целиком содержит окружность, полученную при вращении этой точки вокруг l.
Прямая l называется осью вращения. Линии, полученные при вращении точек поверхности вокруг оси, называются параллелями поверхности вращения. Если точка не принадлежит l, то параллель, проходящая через нее, представляет собой окружность, если же точка принадлежит l, то параллель - совпадает с самой точкой. Ясно, что плоскости, содержащие параллели поверхности, перпендикулярны ее оси. Кривая, полученная при пересечении поверхности вращения с плоскостью, проходящей через ее ось, называется меридианом этой поверхности. Поверхность можно получить, вращая любой ее меридиан вокруг оси.
Теорема 4. Пусть в пространстве дана прямоугольная декартовая система координат  . Если на координатной плоскости Oxz в системе координат
. Если на координатной плоскости Oxz в системе координат 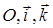 задана кривая g своим уравнением:
задана кривая g своим уравнением:  , то уравнение поверхности, полученной при вращении g вокруг оси Оz в системе координат
, то уравнение поверхности, полученной при вращении g вокруг оси Оz в системе координат  имеют следующий вид:
имеют следующий вид:
 . (2)
. (2)
 Доказательство. Пусть р - данная поверхность вращения, а
Доказательство. Пусть р - данная поверхность вращения, а  - ее произвольная точка (рис. 104). Обозначим через w параллель поверхности р, проходящую через точку М. Она представляет собой окружность. Ее центр находится в точке N оси Оz и радиус равен длине отрезка МN. Так как отрезок MN перпендикулярен оси Оz, то координаты точки N равны:
- ее произвольная точка (рис. 104). Обозначим через w параллель поверхности р, проходящую через точку М. Она представляет собой окружность. Ее центр находится в точке N оси Оz и радиус равен длине отрезка МN. Так как отрезок MN перпендикулярен оси Оz, то координаты точки N равны:  . Поэтому
. Поэтому  . Пусть w пересекает координатную ось Oxz в точках
. Пусть w пересекает координатную ось Oxz в точках  и
и  . Отрезки
. Отрезки  и
и  также перпендикулярны оси Оz, точки
также перпендикулярны оси Оz, точки  и
и  симметричны относительно N, поэтому их координаты равны:
симметричны относительно N, поэтому их координаты равны: 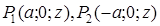 . Но,
. Но,  . Отсюда следует, что
. Отсюда следует, что  . Таким образом,
. Таким образом,  и
и  имеют следующие координаты:
имеют следующие координаты:  . Одна из этих точек принадлежит кривой w, следовательно, либо
. Одна из этих точек принадлежит кривой w, следовательно, либо  , либо
, либо  . Поэтому координаты точки М удовлетворяют уравнению:
. Поэтому координаты точки М удовлетворяют уравнению:  .
.
Обратно, пусть координаты х, у и z некоторой точки М удовлетворяют уравнению (2). Покажем, что она принадлежит поверхности вращения р. Спроектируем М на ось Оz, получим точку N, координаты которой равны:  . Построим окружность w с центром в точке N, радиуса
. Построим окружность w с центром в точке N, радиуса 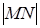 , плоскость которой перпендикулярна оси Оz. Эта окружность пересекает координатную плоскость Oxz в точках
, плоскость которой перпендикулярна оси Оz. Эта окружность пересекает координатную плоскость Oxz в точках  и
и  . Как ранее было доказано, координаты этих точек равны:
. Как ранее было доказано, координаты этих точек равны:  . Из уравнения (25.2) следует, что
. Из уравнения (25.2) следует, что 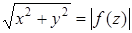 . Если
. Если  , то
, то  и точка
и точка  лежит на кривой w. Если
лежит на кривой w. Если  , то
, то  , в этом случае
, в этом случае  принадлежит w. Таким образом, w ‑ окружность вращения либо точки
принадлежит w. Таким образом, w ‑ окружность вращения либо точки  , либо точки
, либо точки  вокруг оси Оz, поэтому она целиком принадлежит поверхности вращения р. Следовательно, на этой поверхности лежит и точка М. Теорема доказана.
вокруг оси Оz, поэтому она целиком принадлежит поверхности вращения р. Следовательно, на этой поверхности лежит и точка М. Теорема доказана.
Можно доказать, что уравнение поверхности, образованной вращением вокруг оси Оz кривой, принадлежащей плоскости Оуz и определенной в системе уравнением 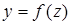 , также совпадает с уравнением (25.2). Аналогично определяются уравнения поверхностей вращения вокруг осей Ox и Оу.
, также совпадает с уравнением (25.2). Аналогично определяются уравнения поверхностей вращения вокруг осей Ox и Оу.
Приведем примеры поверхностей вращения второго порядка
Пример 1. В плоскости Oxz дана прямая, параллельная оси Оz:  . Определить уравнение поверхности, образованной вращением прямой вокруг оси Оz.
. Определить уравнение поверхности, образованной вращением прямой вокруг оси Оz.
Решение. Воспользуемся уравнением (25.2). Так как  , то уравнение поверхности вращения имеет вид
, то уравнение поверхности вращения имеет вид 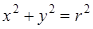 . Эта поверхность, в соответствии с теоремой 2 является цилиндрической. Она носит название кругового цилиндра.
. Эта поверхность, в соответствии с теоремой 2 является цилиндрической. Она носит название кругового цилиндра.
Пример 2. В плоскости Oxz дана прямая, проходящая через начало координат:  . Определить уравнение поверхности, образованной вращением этой прямой вокруг оси Оz.
. Определить уравнение поверхности, образованной вращением этой прямой вокруг оси Оz.
Решение. Как следует из формулы (25.2) искомое уравнение имеет вид:  , или
, или  . Полученная поверхность является конической (см. теорему 3). Ее называют круговым конусом.
. Полученная поверхность является конической (см. теорему 3). Ее называют круговым конусом.
 Пример 3. В плоскости Охz дан эллипс:
Пример 3. В плоскости Охz дан эллипс:  . Определить уравнение, полученное при его вращении вокруг оси Оz.
. Определить уравнение, полученное при его вращении вокруг оси Оz.
Решение. Так как эллипс, определенный своим каноническим уравнением, симметричен относительно начала координат, то для построения поверхности достаточно вращать вокруг оси Оz только его половину, для точек которой абсциссы больше или равны 0. Эта часть эллипса определена уравнением:  . Из формулы (2) следует, что уравнение искомой поверхности можно записать в виде:
. Из формулы (2) следует, что уравнение искомой поверхности можно записать в виде:  или
или  . Такая поверхность называется эллипсоидом вращения. Она представлена на рисунке 105.
. Такая поверхность называется эллипсоидом вращения. Она представлена на рисунке 105.
 Пример 4. В плоскости Oxz дана гипербола:
Пример 4. В плоскости Oxz дана гипербола:  . Определить уравнение поверхности, полученной при вращении вокруг оси Оz.
. Определить уравнение поверхности, полученной при вращении вокруг оси Оz.
Решение. Как следует из уравнения гиперболы, она пересекает ось Ox и не пересекает ось вращения Оz. Исходя из ее свойств симметрии для построения поверхности будем вращать только одну ветвь гиперболы, для точек которой абсцисса положительна. Уравнение этой ветви можно представить в виде: 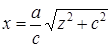 . Используя (2), получим уравнение искомой поверхности вращения
. Используя (2), получим уравнение искомой поверхности вращения  , или
, или  . Такая поверхность называется однополостным гиперболоидом вращения (рис. 106).
. Такая поверхность называется однополостным гиперболоидом вращения (рис. 106).
Пример 5. В плоскости Oxz дана гипербола:  . Определить уравнение поверхности, полученной при ее вращении вокруг оси аппликат.
. Определить уравнение поверхности, полученной при ее вращении вокруг оси аппликат.
 Решение. Данная гипербола пересекает ось Оz и не пересекает оси Ox. Из соображений симметрии будем вращать только ту часть гиперболы, точки которой имеют положительную абсциссу. Уравнение этой части представим в виде:
Решение. Данная гипербола пересекает ось Оz и не пересекает оси Ox. Из соображений симметрии будем вращать только ту часть гиперболы, точки которой имеют положительную абсциссу. Уравнение этой части представим в виде: 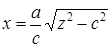 . Поэтому из (2) следует, что уравнение
. Поэтому из (2) следует, что уравнение  служит уравнением искомой поверхности. Преобразуем его к виду:
служит уравнением искомой поверхности. Преобразуем его к виду:  . Полученная поверхность называется двуполостным гиперболоидом вращения (рис. 107).
. Полученная поверхность называется двуполостным гиперболоидом вращения (рис. 107).
 Пример 6. В плоскости Oxz дана парабола
Пример 6. В плоскости Oxz дана парабола  .
.
Найти уравнение поверхности, полученной при ее вращении вокруг оси Оz.
Решение. Искомую поверхность можно получить, вращая только одну ветвь параболы, определенную уравнением  . Из (2) следует, что уравнение поверхности имеет вид:
. Из (2) следует, что уравнение поверхности имеет вид:  .
.
Эта поверхность называется эллиптическим параболоидом вращения. Она изображена на рисунке 108.
Поиск по сайту: