Экстремум функции двух переменных

Функция двух переменных имеет максимум в точке , если для всех точек , достаточно близких к точке и отличных от неё.

Аналогично, функция имеет минимум в точке , если для всех точек , достаточно близких к точке и отличных от неё. Максимумы и минимумы функции называются экстремумами функции.

Необходимые условия экстремума: если функция имеет в точке экстремум, то каждая частная производная первого порядка от в этой точке или равна нулю , , или не существует.

Точки, в которых частные производные и функции равны нулю или не существуют, называются критическими точками этой функции.

Если функция достигает экстремума в какой-либо точке, то это может случиться только в критической точке.

Геометрический смысл равенства нулю частных производных состоит в том, что в точке касательная плоскость к поверхности параллельна плоскости Оxy.

Однако не всякая критическая точка является точкой экстремума. Например, функция имеет критическую точку , так как , , но эта функция при указанных значениях не имеет ни максимума, ни минимума. Действительно, эта функция равна нулю в точке , но в её окрестности есть как положительные, так и отрицательные значения функции . Следовательно, значение нуль не является ни максимумом, ни минимумом.

Для исследования функции в критических точках установим достаточные условия экстремума функции двух переменных.

Пусть функция имеет критическую точку , т.е. 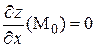, и в некоторой окрестности точки функция имеет частные производные второго порядка: ; ; , тогда:

1) Если , то в точке функция имеет экстремум (максимум при и минимум при );

2) Если , то в точке функция не имеет ни максимума, ни минимум.

3) Если 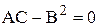, то экстремум может быть и может ни быть. В этом случае требуется дальнейшее исследование

Пример 1. Исследовать на экстремум функцию .

Решение:Критические точки функции двух переменных находятся из системы уравнений: и (необходимые условия экстремума).

Найдём частные производные первого порядка:

; .

Система уравнений для определения критических точек заданной функции примет вид:

.

Для решения системы из первого уравнения выразим , и подставим эту формулу во второе уравнение, получим или и . Находим значение , соответствующее значению . Из уравнения имеем . Получим критическую точку . Найдем вторые частные производные ; ; .

Так как , значит, в точке функция имеет экстремум. Поскольку , то функция имеет максимум. Вычислим значение функции в точке .

12.5 Абсолютный и условный экстремумы. Классические методы оптимизации

Рассмотрим некоторое множество G точек плоскости.

Точка М называется внутренней для множества G, если она принадлежит этому множеству вместе с некоторой своей окрестностью (рисунок 8).

Точка N называется границей для множества G, если в любой её полной окрестности имеются точки, как принадлежащие G, так и не принадлежащие ему.

Совокупность всех граничных точек множества G называется его границей Г.

Множество с присоединенной границей Г называется замкнутой областью. В качестве последней можно рассматривать совокупность точек плоскости, для которых .

Определение1. Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции.

Теорема Вейерштрасса. Функция, непрерывна в ограниченной и замкнутой области, достигает в этой области своего наименьшего и своего наибольшего значения.

Теорема. Абсолютный экстремум функции в данной области достигается либо в критической точке функции, принадлежащей этой области, либо в граничной точке области.

Пример 1. Найти абсолютный экстремум функции в треугольной области S с вершинами .

Решение:Имеем , .

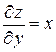Отсюда критическая точка О(0; 0) с координатами и принадлежит области S. Изучим поведение функции на границе области S.

На участке ОА имеем . Поэтому . Аналогично, на участке ОВ: и получаем z.

Найдём уравнение прямой АВ с известными координатами точек А и В: или или . Отсюда - есть функция одной переменной x и, следовательно, имеем при , тогда .

Так как , то в точке функция z достигает своего наибольшего значения на отрезке АВ.

Итак, наименьшее значение функции в области S – есть и оно реализуется в точках отрезков ОА и ОВ. Наибольшее значение достигается в точке на отрезке АВ.

Для нахождения наибольшего и наименьшего значений функции в замкнутой ограниченной области нужно:

1) найти критические точки функции;

2) отобрать те из них, которые лежат внутри заданной области;

3) для каждого участка границы области (используя его уравнение) представить функцию , как функцию одной переменной и найти критические точки полученных функций;

4) Вычислить значения функции в критических точках внутри и на границе области, сравнить их значения и выбрать среди них наибольшее и наименьшее.

Во многих задачах на разыскание наибольших и наименьших значений функции вопрос сводится к разыскиванию максимумов и минимумов функции от нескольких переменных, которые не являются независимыми, а связаны друг с другом некоторыми условиями (например, уравнением связи). В этом случае мы имеем задачу на условный экстремум.

Пусть требуется найти максимумы и минимумы функции при условии, что переменные и связаны соотношением .

Для отыскивания условного экстремума функции методом множителей Лагранжа при наличии одного уравнения связи нужно:

1. Составить функцию Лагранжа , где - множитель Лагранжа;

2. Решить систему уравнений: ; ; , позволяющую найти точки возможного экстремума функции ;

3. С помощью достаточного условия экстремума проверить наличие экстремума функции в каждой точке ;

4. Записать значение условного экстремума исходной функции.

Пример 2. Найти экстремум функции , при условии, что и связаны уравнением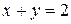

Решение.Рассмотрим функцию Лагранжа . Найдём частные производные 1-го порядка для данной функции: и . Из системы уравнений (необходимые условия экстремумов)

, находим , , .

Найдём вторые частные производные и их значения в точке для функции Лагранжа: ; ; . Так как и при этом , следовательно, при данном уравнении связи функция имеет минимум .

Задача о нахождении наименьшего и наибольшего значений линейной функции возникает при решении ряда экономико-производственных задач, когда требуется составить оптимальный план выпуска продукции предприятием, обеспечивающий максимальную производительность процесса или минимальные затраты сырья и т.д.

Для того чтобы применить математические методы решения к экономическим задачам необходимо переложить экономическую задачу на язык математики, т.е. составить математическую модель задачи. Рассмотрим, например, задачу об оптимальном использовании ресурсов. Пусть предприятие выпускает два вида изделий (шкафы и буфеты). Для их производства требуется четыре вида ресурсов (I-полированные доски; II- древесно-стружечные плиты; III-дополнительные материалы; IV-энергомашинные и людские ресурсы). Эти ресурсы ограничены и составляют на данный момент соответственно условных единиц. Известны технологические коэффициенты которые показывают сколько единиц -го ресурса необходимо для изготовления одной единицы -го вида изделий Известна прибыль

Получаемая предприятием при реализации единицы изделия -го вида. Предполагается, что - постоянные величины. Требуется составить такой план выпуска продукции, при котором прибыль предприятия от ее реализации была бы наибольшей. Составим таблицу:

Виды ресурсов	Запасы Ресурсов	Виды изделий
1- Шкафы	2- Буфеты
I	b =120
II	b =160
III	b =120
IV	b =80
ПРИБЫЛЬ

Пусть предприятие планирует выпустить:

х – количество шкафов, у – количество буфетов.

Тогда - количество единиц I-го ресурса, затраченное на изготовление всех планируемых шкафов и буфетов. Поскольку запас I – го ресурса ограничен то должно выполняться неравенство или Аналогично, составляя для каждого вида ресурсов соответствующие неравенства, получим систему ограничений:

Здесь учтено, что переменные х и у должны быть неотрицательными. Прибыль z, получаемая предприятием от реализации х шкафов у буфетов равна: или Функция z является линейной функцией двух переменных и называется целевой функцией. Первые четыре неравенства в системе ограничений принято называть специальными ограничениями задачи математического программирования, а неравенства и - общими ограничениями. Требуется найти наибольшее значение этой функции в области D. Эта задача решается графическим методом.

Алгоритм решения:

1. Построим область допустимых решений D, определяемую системой неравенств;

2. Нанесем на чертеж одну из линий уровня (C – const), пересекающую область допустимых решений D, и градиент функции z, т.е. вектор , расположенный перпендикулярно линии уровня.

3. Передвигаем линию уровня параллельно самой себе в направлении вектора градиента до тех пор пока точки этой линии принадлежат области D, т.е. до некоторой угловой точки, в которой функция z достигает своего наибольшего значения.

Заметим, что в задачах, в которых целевая функция z определяет, например, затраты на производство продукции, требуется найти наименьшее значение функции z при заданных ограничениях, поэтому линию уровня следует передвигать в направлении, противоположном направлению вектора градиента .

Если целевая функция z является функцией более двух переменных, то графический метод неприменим.

Поиск по сайту: