 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Доказательство. Пусть f¢(x1) = 0 и f¢¢(x1)<0
|
Читайте также: |
Пусть f¢(x1) = 0 и f¢¢(x1)<0. Т.к. функция f(x) непрерывна, то f¢¢(x1) будет отрицательной и в некоторой малой окрестности точки х1.
Т.к. f¢¢(x) = (f¢(x))¢ < 0, то f¢(x) убывает на отрезке, содержащем точку х1, но f¢(x1)=0, т.е. f¢(x) > 0 при х<x1 и f¢(x) < 0 при x>x1. Это и означает, что при переходе через точку х = х1 производная f¢(x) меняет знак с “+” на “-“, т.е. в этой точке функция f(x) имеет максимум.
Для случая минимума функции теорема доказывается аналогично.
Если f¢¢(x) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.
Выпуклость и вогнутость кривой.
Точки перегиба.
Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.
 у
у
x
На рисунке показана иллюстрация приведенного выше определения.
Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).
Доказательство. Пусть х0 Î (a, b). Проведем касательную к кривой в этой точке.
Уравнение кривой: y = f(x);
Уравнение касательной: 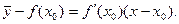
Следует доказать, что  .
.
По теореме Лагранжа для f(x) – f(x0):  , x0 < c < x.
, x0 < c < x.
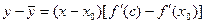
По теореме Лагранжа для 

Пусть х > x0 тогда x0 < c1 < c < x. Т.к. x – x0 > 0 и c – x0 > 0, и кроме того по условию
 , следовательно,
, следовательно,  .
.
Пусть x < x0 тогда x < c < c1 < x0 и x – x0 < 0, c – x0 < 0, т.к. по условию  то
то
 .
.
Аналогично доказывается, что если f¢¢(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).
Теорема доказана.
Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная пересекает кривую.
Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
Доказательство. 1) Пусть f¢¢(x) < 0 при х < a и f¢¢(x) > 0 при x > a. Тогда при
x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба.
2) Пусть f¢¢(x) > 0 при x < b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.
Теорема доказана.
Асимптоты.
При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.
Определение. Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.
Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.
Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике функции  . Ее наклонная асимптота у = х.
. Ее наклонная асимптота у = х.

Рассмотрим подробнее методы нахождения асимптот кривых.
Вертикальные асимптоты.
Из определения асимптоты следует, что если  или
или  или
или 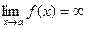 , то прямая х = а – асимптота кривой y = f(x).
, то прямая х = а – асимптота кривой y = f(x).
Например, для функции  прямая х = 5 является вертикальной асимптотой.
прямая х = 5 является вертикальной асимптотой.
Наклонные асимптоты.
Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b.




 M
M
 |
j
N
j P
Q
Обозначим точку пересечения кривой и перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью Ох обозначим j. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N.
Тогда MQ = y – ордината точки кривой, NQ =  - ордината точки N на асимптоте.
- ордината точки N на асимптоте.
По условию:  , ÐNMP = j,
, ÐNMP = j,  .
.
Угол j - постоянный и не равный 900, тогда


Тогда  .
.
Итак, прямая y = kx + b – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.
В полученном выражении выносим за скобки х:

Т.к. х®¥, то  , т.к. b = const, то
, т.к. b = const, то  .
.
Тогда  , следовательно,
, следовательно,

 .
.
Т.к.  , то
, то 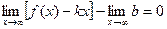 , следовательно,
, следовательно,


Отметим, что горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0.
Пример. Найти асимптоты и построить график функции  .
.
1) Вертикальные асимптоты: y®+¥ x®0-0: y®-¥ x®0+0, следовательно, х = 0- вертикальная асимптота.
2) Наклонные асимптоты:
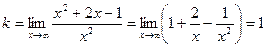

Таким образом, прямая у = х + 2 является наклонной асимптотой.
Построим график функции:

Пример. Найти асимптоты и построить график функции  .
.
Прямые х = 3 и х = -3 являются вертикальными асимптотами кривой.
Найдем наклонные асимптоты: 

y = 0 – горизонтальная асимптота.

Пример. Найти асимптоты и построить график функции  .
.
Прямая х = -2 является вертикальной асимптотой кривой.
Найдем наклонные асимптоты.


Итого, прямая у = х – 4 является наклонной асимптотой.

Схема исследования функций
Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать:
1) Область существования функции.
Это понятие включает в себя и область значений и область определения функции.
2) Точки разрыва. (Если они имеются).
3) Интервалы возрастания и убывания.
4) Точки максимума и минимума.
5) Максимальное и минимальное значение функции на ее области определения.
6) Области выпуклости и вогнутости.
7) Точки перегиба.(Если они имеются).
8) Асимптоты.(Если они имеются).
9) Построение графика.
Применение этой схемы рассмотрим на примере.
Пример. Исследовать функцию  и построить ее график.
и построить ее график.
Находим область существования функции. Очевидно, что областью определения функции является область (-¥; -1) È (-1; 1) È (1; ¥).
В свою очередь, видно, что прямые х = 1, х = -1 являются вертикальными асимптотами кривой.
Областью значений данной функции является интервал (-¥; ¥).
Точками разрыва функции являются точки х = 1, х = -1.
Находим критические точки.
Найдем производную функции

Критические точки: x = 0; x = -  ; x =
; x =  ; x = -1; x = 1.
; x = -1; x = 1.
Найдем вторую производную функции



 .
.
Определим выпуклость и вогнутость кривой на промежутках.
-¥ < x < -  , y¢¢ < 0, кривая выпуклая
, y¢¢ < 0, кривая выпуклая
-  < x < -1, y¢¢ < 0, кривая выпуклая
< x < -1, y¢¢ < 0, кривая выпуклая
-1 < x < 0, y¢¢ > 0, кривая вогнутая
0 < x < 1, y¢¢ < 0, кривая выпуклая
1 < x <  , y¢¢ > 0, кривая вогнутая
, y¢¢ > 0, кривая вогнутая
 < x < ¥, y¢¢ > 0, кривая вогнутая
< x < ¥, y¢¢ > 0, кривая вогнутая
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
-¥ < x < -  , y¢ > 0, функция возрастает
, y¢ > 0, функция возрастает
-  < x < -1, y¢ < 0, функция убывает
< x < -1, y¢ < 0, функция убывает
-1 < x < 0, y¢ < 0, функция убывает
0 < x < 1, y¢ < 0, функция убывает
1 < x <  , y¢ < 0, функция убывает
, y¢ < 0, функция убывает
 < x < ¥, y¢¢ > 0, функция возрастает
< x < ¥, y¢¢ > 0, функция возрастает
Видно, что точка х = -  является точкой максимума, а точка х =
является точкой максимума, а точка х =  является точкой минимума. Значения функции в этих точках равны соответственно 3
является точкой минимума. Значения функции в этих точках равны соответственно 3  /2 и -3
/2 и -3  /2.
/2.
Про вертикальные асимптоты было уже сказано выше. Теперь найдем наклонные асимптоты.


Итого, уравнение наклонной асимптоты – y = x.
Построим график функции:

При использовании компьютерной версии “ Курса высшей математики ” возможно запустить программу, которая проводит полное исследование функций по приведенной выше схеме. Достаточно ввести функцию, программа выведет подробный отчет о результатах исследования по каждому пункту.
Для запуска программы дважды щелкните по значку:
 |
Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
Векторная функция скалярного аргумента.
 z
z
A(x, y, z)



y
х
Пусть некоторая кривая в пространстве задана параметрически:
x = j(t); y = y(t); z = f(t);
Радиус- вектор произвольной точки кривой:  .
.
Таким образом, радиус- вектор точки кривой может рассматриваться как некоторая векторная функция скалярного аргумента t. При изменении параметра t изменяется величина и направление вектора  .
.
Запишем соотношения для некоторой точки t0:

Тогда вектор  - предел функции
- предел функции  (t).
(t).  .
.
Очевидно, что
 , тогда
, тогда
 .
.
Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.
 |




 ;
;  ;
;


или, если существуют производные j¢(t), y¢(t), f¢(t), то

Это выражение – вектор производная вектора  .
.


Если имеется уравнение кривой:
x = j(t); y = y(t); z = f(t);
то в произвольной точке кривой А(xА, yА, zА) с радиус- вектором

можно провести прямую с уравнением 
Т.к. производная  - вектор, направленный по касательной к кривой, то
- вектор, направленный по касательной к кривой, то
 .
.
Свойства производной векторной функции скалярного аргумента.
1) 
2)  , где l = l(t) – скалярная функция
, где l = l(t) – скалярная функция
3) 
4) 
Уравнение нормальной плоскости к кривой будет иметь вид:

Пример. Составить уравнения касательной и нормальной плоскости к линии, заданной уравнением  в точке t = p/2.
в точке t = p/2.
Уравнения, описывающие кривую, по осям координат имеют вид:
x(t) = cost; y(t) = sint; z(t) =  ;
;
Находим значения функций и их производных в заданной точке:
x¢(t) = -sint; y¢(t) = cost; 
x¢(p/2) = -1; y¢(p/2) = 0; z¢(p/2)= 
x(p/2) = 0; y(p/2) = 1; z¢(p/2)= p  /2
/2

- это уравнение касательной.
Нормальная плоскость имеет уравнение:
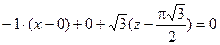

Параметрическое задание функции.
Исследование и построение графика кривой, которая задана системой уравнений вида:
 ,
,
производится в общем то аналогично исследованию функции вида y = f(x).
Находим производные:

Теперь можно найти производную  . Далее находятся значения параметра t, при которых хотя бы одна из производных j¢(t) или y¢(t) равна нулю или не существует. Такие значения параметра t называются критическими.
. Далее находятся значения параметра t, при которых хотя бы одна из производных j¢(t) или y¢(t) равна нулю или не существует. Такие значения параметра t называются критическими.
Для каждого интервала (t1, t2), (t2, t3), …, (tk-1, tk) находим соответствующий интервал (x1, x2), (x2, x3), …, (xk-1, xk) и определяем знак производной  на каждом из полученных интервалов, тем самым определяя промежутки возрастания и убывания функции.
на каждом из полученных интервалов, тем самым определяя промежутки возрастания и убывания функции.
Далее находим вторую производную функции на каждом из интервалов и, определяя ее знак, находим направление выпуклости кривой в каждой точке.
Для нахождения асимптот находим такие значения t, при приближении к которым или х или у стремится к бесконечности, и такие значения t, при приближении к которым и х и у стремится к бесконечности.
В остальном исследование производится аналогичным также, как и исследование функции, заданной непосредственно.
На практике исследование параметрически заданных функций осуществляется, например, при нахождении траектории движущегося объекта, где роль параметра t выполняет время.
Ниже рассмотрим подробнее некоторые широко известные типы параметрически заданных кривых.
Уравнения некоторых типов кривых в параметрической
форме.
 Окружность.
Окружность.
Если центр окружности находится в начале координат, то координаты любой ее
точки могут быть найдены по формулам:
 0 £ t £ 3600
0 £ t £ 3600
Если исключить параметр t, то получим каноническое уравнение окружности:
x2 + y2 = r2(cos2t + sin2t) = r2
Эллипс.
 Каноническое уравнение:
Каноническое уравнение:  .
.
В
C M(x, y)
t
О N P
Для произвольной точки эллипса М(х, у) из геометрических соображений можно записать:  из DОВР и
из DОВР и  из DOCN, где а- большая полуось эллипса, а b- меньшая полуось эллипса, х и у – координаты точки М.
из DOCN, где а- большая полуось эллипса, а b- меньшая полуось эллипса, х и у – координаты точки М.
Тогда получаем параметрические уравнения эллипса:

где 0 £ t £ 2p
Угол t называется эксцентрическим углом.
Циклоида.
у

С
М К
О Р В pа 2pа х
Определение. Циклоидой называется кривая, которую описывает некоторая точка, лежащая на окружности, когда окружность без скольжения катится по прямой.
Пусть окружность радиуса а перемещается без скольжения вдоль оси х. Тогда из геометрических соображений можно записать: OB =  = at; PB = MK = asint;
= at; PB = MK = asint;
ÐMCB = t; Тогда y = MP = KB = CB – CK = a – acost = a(1 – cost).
x = at – asint = a(t – sint).
Итого:  при 0 £ t £ 2p - это параметрическое уравнение циклоиды.
при 0 £ t £ 2p - это параметрическое уравнение циклоиды.
Если исключить параметр, то получаем:


Как видно, параметрическое уравнение циклоиды намного удобнее в использовании, чем уравнение, непосредственно выражающее одну координату через другую.
Астроида.
Данная кривая представляет собой траекторию точки окружности радиуса R/4, вращающейся без скольжения по внутренней стороне окружности радиуса R.
 |
R/4
R
Параметрические уравнения, задающие изображенную выше кривую,
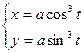 , 0 £ t £ 2p,
, 0 £ t £ 2p,
Преобразуя, получим: x2/3 + y2/3 = a2/3(cos2t + sin2t) = a2/3
Производная функции, заданной параметрически.
Пусть 
Предположим, что эти функции имеют производные и функция x = j(t) имеет обратную функцию t = Ф(х).
Тогда функция у = y(t) может быть рассмотрена как сложная функция y = y[Ф(х)].

т.к. Ф(х) – обратная функция, то 
Окончательно получаем: 
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.
Пример. Найти производную функции 
Способ 1: Выразим одну переменную через другую  , тогда
, тогда

Способ 2: Применим параметрическое задание данной кривой:  .
.

x2 = a2cos2t; 


Кривизна плоской кривой.
 |
a a
В
А А В
Определение: Угол a поворота касательной к кривой при переходе от точки А к точке В называется углом смежности.
Соответственно, более изогнута та кривая, у которой при одинаковой длине больше угол смежности.
Определение: Средней кривизной Кср дуги  называется отношение соответствующего угла смежности a к длине дуги
называется отношение соответствующего угла смежности a к длине дуги  .
.

Отметим, что для одной кривой средняя кривизна ее различных частей может быть различной, т.е. данная величина характеризует не кривую целиком, а некоторый ее участок.
Определение: Кривизной дуги в точке КА называется предел средней кривизны при стремлении длины дуги  ® 0.
® 0.

Легко видеть, что если обозначить  = S, то при условии, что угол a - функция, которая зависит от S и дифференцируема, то
= S, то при условии, что угол a - функция, которая зависит от S и дифференцируема, то

Определение: Радиусом кривизны кривой называется величина  .
.
Пусть кривая задана уравнением y = f(x).
 y
y
B
Dj
A j j+Dj
x
Kcp =  ;
;  ;
;
Если j = j(x) и S = S(x), то  .
.
В то же время  .
.
Для дифференциала дуги:  , тогда
, тогда

Т.к.  . В других обозначениях:
. В других обозначениях:  .
.
Рассмотрим кривую, заданную уравнением: y = f(x).
 |
A
C(a, b)
Если построить в точке А кривой нормаль, направленную в сторону выпуклости, то можно отложить отрезок АС = R, где R – радиус кривизны кривой в точке А. Тогда точка С(a, b) называется центром кривизны кривой в точке А.
Круг радиуса R с центром в точке С называется кругом кривизны.
Очевидно, что в точке А кривизна кривой и кривизна окружности равны.
Можно показать, что координаты центра кривизны могут быть найдены по формулам:

Определение: Совокупность всех центров кривизны кривой линии образуют новую линию, которая называется эволютой по отношению к данной кривой. По отношению к эволюте исходная кривая называется эвольвентой.
Приведенные выше уравнения, определяющие координаты центров кривизны кривой определяют уравнение эволюты.
Свойства эволюты.
Теорема 1: Нормаль к данной кривой является касательной к ее эволюте.
Теорема 2: Модуль разности радиусов кривизны в любых точках кривой равен модулю длины соответствующей эволюты.
 С3
С3
С2 
С1 
R1 R2 R3
M1
M’1 M2 M3
M’2
M’3
Надо отметить, что какой – либо эволюте соответствует бесконечное число эвольвент.
Указанные выше свойства можно проиллюстрировать следующим образом: если на эволюту натянута нить, то эвольвента получается как траекторная линия конца нити при ее сматывании или разматывании при условии, что нить находится в натянутом состоянии.
Пример: Найти уравнение эволюты кривой, заданной уравнениями:




Уравнения эволюты: 
Окончательно:  - это уравнения окружности с центром в начале координат радиуса а. Исходная кривая получается своего рода разверткой окружности.
- это уравнения окружности с центром в начале координат радиуса а. Исходная кривая получается своего рода разверткой окружности.
Ниже приведены графики исходной кривой и ее эволюты.

Кривизна пространственной кривой.
 z
z
A(x, y, z)
B 


0 y
x
Для произвольной точки А, находящейся на пространственной кривой, координаты могут быть определены как функции некоторой длины дуги S.
x = j(S); y = y(S); z = f(S);

Приведенное выше уравнение называют векторным уравнением линии в пространстве.
Определение: Линия, которую опишет в пространстве переменный радиус – вектор  при изменении параметра S, называется годографом этого вектора.
при изменении параметра S, называется годографом этого вектора.
 , тогда
, тогда  - вектор, направленный по касательной к кривой в точке А(x, y, z).
- вектор, направленный по касательной к кривой в точке А(x, y, z).
Но т.к.  , то
, то  - единичный вектор, направленный по касательной.
- единичный вектор, направленный по касательной.
Если принять  , то
, то  .
.
Причем  .
.
Рассмотрим вторую производную 
Определение: Прямая, имеющая направление вектора  называется главной нормалью к кривой. Ее единичный вектор обозначается
называется главной нормалью к кривой. Ее единичный вектор обозначается  .
.
 , где К – кривизна кривой.
, где К – кривизна кривой.

Кривизна пространственной кривой может быть найдена по формуле:

Возможна и другая запись формулы для кривизны пространственной кривой (она получается из приведенной выше формулы):

Определение: Вектор  называется вектором кривизны. Величина
называется вектором кривизны. Величина  называется радиусом кривизны.
называется радиусом кривизны.
О формулах Френе.
Формулами Френе называются соотношения:


Последняя формула получена из двух первых.
В этих формулах:
 - единичный вектор главной нормали к кривой,
- единичный вектор главной нормали к кривой,
 - единичный вектор бинормали,
- единичный вектор бинормали,
R – радиус кривизны кривой  ,
,
Т – радиус кручения кривой.
Определение: Плоскость, проходящая через касательную и главную нормаль к кривой в точке А называется соприкасающейся плоскостью.
Определение: Нормаль к кривой, перпендикулярная к соприкасающейся плоскости, называется бинормалью. Ее единичный вектор-  .
.

Величина  называется кручением кривой.
называется кручением кривой.
Ниже рассмотрим несколько примеров исследования методами дифференциального исчисления различных типов функций.
Пример: Методами дифференциального исчисления исследовать функцию  и построить ее график.
и построить ее график.
1. Областью определения данной функции являются все действительные числа (-¥; ¥).
2. Функция является функцией общего вида в смысле четности и нечетности.
3. Точки пересечения с координатными осями: c осью Оу: x = 0; y = 1;
с осью Ох: y = 0; x = 1;
4. Точки разрыва и асимптоты: Вертикальных асимптот нет.
Наклонные асимптоты: общее уравнение y = kx + b;


Итого: у = -х – наклонная асимптота.
5. Возрастание и убывание функции, точки экстремума.
 . Видно, что у¢< 0 при любом х ¹ 0, следовательно, функция убывает на всей области определения и не имеет экстремумов. В точке х = 0 первая производная функции равна нулю, однако в этой точке убывание не сменяется на возрастание, следовательно, в точке х = 0 функция скорее всего имеет перегиб. Для нахождения точек перегиба, находим вторую производную функции.
. Видно, что у¢< 0 при любом х ¹ 0, следовательно, функция убывает на всей области определения и не имеет экстремумов. В точке х = 0 первая производная функции равна нулю, однако в этой точке убывание не сменяется на возрастание, следовательно, в точке х = 0 функция скорее всего имеет перегиб. Для нахождения точек перегиба, находим вторую производную функции.
 y¢¢ = 0 при х =0 и y¢¢ = ¥ при х = 1.
y¢¢ = 0 при х =0 и y¢¢ = ¥ при х = 1.
Точки (0,1) и (1,0) являются точками перегиба, т.к. y¢¢(1-h) < 0; y¢¢(1+h) >0; y¢¢(-h) > 0; y¢¢(h) < 0 для любого h > 0.
6. Построим график функции.

Пример: Исследовать функцию  и построить ее график.
и построить ее график.
1. Областью определения функции являются все значения х, кроме х = 0.
2. Функция является функцией общего вида в смысле четности и нечетности.
3. Точки пересечения с координатными осями: c осью Ох: y = 0; x = 
с осью Оу: x = 0; y – не существует.
4. Точка х = 0 является точкой разрыва  , следовательно, прямая х = 0 является вертикальной асимптотой.
, следовательно, прямая х = 0 является вертикальной асимптотой.
Наклонные асимптоты ищем в виде: y = kx + b.


Наклонная асимптота у = х.
5. Находим точки экстремума функции.
 ; y¢ = 0 при х = 2, у¢ = ¥ при х = 0.
; y¢ = 0 при х = 2, у¢ = ¥ при х = 0.
y¢ > 0 при х Î (-¥, 0) – функция возрастает,
y¢ < 0 при х Î (0, 2) – функция убывает,
у¢ > 0 при х Î (2, ¥) – функция возрастает.
Таким образом, точка (2, 3) является точкой минимума.
Для определения характера выпуклости/вогнутости функции находим вторую производную.
 > 0 при любом х ¹ 0, следовательно, функция вогнутая на всей области определения.
> 0 при любом х ¹ 0, следовательно, функция вогнутая на всей области определения.
6. Построим график функции.

Пример: Исследовать функцию  и построить ее график.
и построить ее график.
1. Областью определения данной функции является промежуток х Î (-¥, ¥).
2. В смысле четности и нечетности функция является функцией общего вида.
3. Точки пересечения с осями координат: с осью Оу: x = 0, y = 0;
с осью Ох: y = 0, x = 0, x = 1.
4. Асимптоты кривой.
Вертикальных асимптот нет.
Попробуем найти наклонные асимптоты в виде y = kx + b.
 - наклонных асимптот не существует.
- наклонных асимптот не существует.
5. Находим точки экстремума.

Для нахождения критических точек следует решить уравнение 4х3 – 9х2 +6х –1 = 0.
Для этого разложим данный многочлен третьей степени на множители.
Подбором можно определить, что одним из корней этого уравнения является число
х = 1. Тогда:
 4x3 – 9x2 + 6x – 1 x - 1
4x3 – 9x2 + 6x – 1 x - 1
` 4x3 – 4x2 4x2 – 5x + 1
- 5x2 + 6x
` - 5x2 + 5x
x - 1
` x - 1
Тогда можно записать (х – 1)(4х2 – 5х + 1) = 0. Окончательно получаем две критические точки: x = 1 и x = ¼.
Примечание. Операции деления многочленов можно было избежать, если при нахождении производной воспользоваться формулой производной произведения:

Найдем вторую производную функции: 12x2 – 18x + 6. Приравнивая к нулю, находим:
x = 1, x = ½.
Систематизируем полученную информацию в таблице:
| (-¥; ¼) | 1/4 | (¼; ½) | 1/2 | (½; 1) | (1; ¥) | ||
| f¢¢(x) | + | + | + | - | + | ||
| f¢(x) | - | + | + | + | + | ||
| f(x) | убывает вып.вниз | min | возрастает вып.вниз | перегиб | возрастает вып.вверх | перегиб | возрастает вып. вниз |
6. Построим график функции.

Интегральное исчисление.
Первообразная функция.
Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Неопределенный интеграл.
Определение: Неопределенным интегралом функции f(x) называется множество всех первообразных функций F(x), таких, что
F¢(x) = f(x).
Обозначение: 
Теорема. Если функция f(x) непрерывна на отрезке, то существует неопределенный интеграл на этом отрезке
Свойства:
-1. 
2. 
3. 
4.  где u, v – некоторые функции от х.
где u, v – некоторые функции от х.
5. 
6. 
Пример: 
| Интеграл | Значение | Интеграл | Значение | ||

|  - -
| 
| tgx + C | ||

| 
| 
| - ctgx + C | ||

| 
| 
| arcsin  + C + C
| ||

| ex + C | 
| 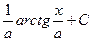
| ||

| - cosx + C | 13 | 
| 
| |

| sinx + C | 14 | 
| 
| |
| 7 | 
| - ln½cosx½+C | 15 | 
| 
|
| 8 | 
| ln½sinx½+ C | 16 | 
| 
|
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на использовании свойств интегралов таблицы интегралов и таблицы производных.
Пример.  .
.
Из формулы дифференцирования 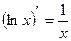 можно сделать вывод, что искомый интеграл равен
можно сделать вывод, что искомый интеграл равен  , где С – некоторое постоянное число. Однако,
, где С – некоторое постоянное число. Однако,  . Таким образом, окончательно получим:
. Таким образом, окончательно получим:

Способ подстановки (замены переменных).
Теорема: Если существуют интегралы  и
и  , то имеет место равенство:
, то имеет место равенство:
 , (*)
, (*)
где x = j(t) и dx = j¢(t)dt.
Доказательство: Продифференцируем (*):

По свойству №2 неопределенного интеграла:
f(x)dx = f[j(t)]j¢(t)dt
следовательно, с учетом введенных обозначений получим справедливость (*). Теорема доказана.
Пример.

Сделаем замену  .
.
Короче получится, если использовать свойство 6.
Пример. 
Замена  Получаем:
Получаем:

Пример. Найти неопределенный интеграл  .
.
Сделаем замену t = sinx, dt = cosxdt.

Пример.


Пример.

Интегрирование по частям.
Способ основан на следующей формуле
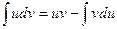 , (**)
, (**)
Доказательство. Дифференциал произведения:
d(uv) = udv + vdu
Проинтегрировав, получаем:
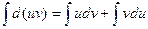 .
.
Далее по свойствам неопределенного интеграла:
 или
или 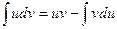 ;
;
Что и требовалось доказать.
Пример. 
 Пример.
Пример.
 Пример.
Пример.

Пример.

Пример. 

Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.


Некоторые примеры.
Пример.

Пример.

Пример.

Интегрирование элементарных дробей.
Определение: Элементарными называются дроби следующих четырех типов:
I.  III.
III. 
II.  IV.
IV. 
m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
I. 
II. 
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида III может быть представлен в виде:
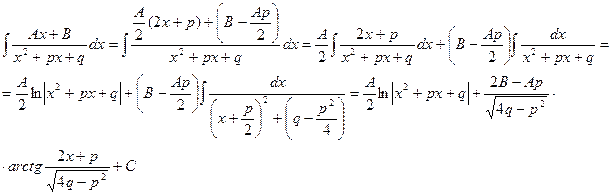
Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
Рассмотрим применение указанной выше формулы на примерах.
Пример.

Вообще говоря, если у трехчлена ax2 + bx + c выражение b2 – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.
Пример.

Пример.

Пример.

Рассмотрим теперь методы интегрирования простейших дробей IV типа.
Сначала рассмотрим частный случай при М = 0, N = 1.
Тогда интеграл вида  можно путем выделения в знаменателе полного квадрата представить в виде
можно путем выделения в знаменателе полного квадрата представить в виде  . Сделаем следующее преобразование:
. Сделаем следующее преобразование:
 .
.
Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим: 

Для исходного интеграла получаем:


Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл  .
.
Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.

В полученном равенстве первый интеграл с помощью подстановки t = u2 + s приводится к табличному  , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
, а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
Поиск по сайту: