Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид

y'' + py' +qy = f(x)

Для нахождения общего решения этого уравнения нужно найти общее решение 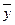однородного уравнения, как это было показано в предыдущем параграфе, и какое-либо частное решение у* неоднородного уравнения. Их сумма будет общим решением данного неоднородного уравнения:

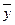у = + у*.

Рассмотрим один из методов нахождения частного решения – метод неопределенных коэффициентов.

Суть метода заключается в следующем: если правая часть уравнения неоднородного уравнения имеет вид

f(x)=e^αx[P_n(x)cosβx + Q_m(x)sinβх],

где α и β – действительные числа, а P_n(x) и Q_m(x) – многочлены соответственно n - йи m – й степени с действительными коэффициентами, то частное решение у* ищется в виде

y* = x^l e^αx[M_s(x)cosβx+N_s(x)sinβx],

где M_s(x) и N_s(x) – многочлены степени s = max(n,m) с неопределенными буквенными коэффициентами, а l – кратность, с которой α + βi входит в число корней характеристического уравнения.

Следует отметить, что в общем виде многочлены соответствующей степени, имеют вид:

- многочлен 0-ой степени - А

- многочлен 1-ой степени - Ах+В

- многочлен 2-ой степени - Ах²+Вх+С

- многочлен 3-ей степени - Ах³+Вх²+Сх+D и т.д.

А, В, С, D, … - неопределенные коэффициенты.

Для того, чтобы найти неопределенные коэффициенты, частное решение у*, его производные у^*' и у^*'' подставляют в левую часть неоднородного уравнения и производят соответствующие упрощения; затем в полученном тождестве приравнивают коэффициенты при подобных членах в левой и правой частях, что дает систему уравнений относительно искомых неопределенных коэффициентов, решив которую находят эти коэффициенты.

Замечание. Если правая часть неоднородного уравнения есть сумма функций вида

f(x)=f₁(x)+f₂(x)+ … +f_n(x),

нужно предварительно найти частные решения y₁*, y₂*, …,y_n*, соответствующие функциям f₁(x, f₂(x), …,f_n(x). Тогда частное решение данного уравнения запишутся в виде

y*= y₁*+ y₂*+, …,+ y_n*.

Более общим методом решения уравнений является метод вариации произвольных постоянных.

Пусть у₁ и у₂ – линейно независимые частные решения однородного уравнения. Тогда общее решение неоднородного уравнения следует искать в виде

у=С₁(х)у₁+С₂(х)у₂

где функции С₁(х) и С₂(х) определяются из системы уравнений

Решая эту систему, получим

,

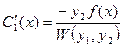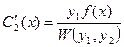
где 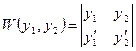- определитель Вронского.

Интегрируя С^'₁(х) и С^'₂(х) получаем

,

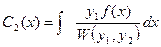откуда, подставляя найденные функции в функцию решения, найдем общее решение линейного неоднородного уравнения.

Пример 10.12. Найти общее решение дифференциального уравнения

y"+4y'=-2xe^-4х.

Решение. Общее решение неоднородного уравнения равно сумме общего решения 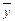однородного уравнения и какого-либо частного решения у* неоднородного уравнения:

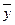у = + у*.

Найдем общее решение однородного уравнения

y"+4y'=0.

Составим характеристическое уравнение и решим его

k² + 4k = 0, k₁=0, k₂=-4.

Общее решение однородного уравнения имеет вид

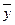= С₁ +C₂e^-4х.

Перейдем к отысканию частного решения у* данного уравнения. Здесь правая часть неоднородного уравнения f(x)=-2xe^-4x содержит произведение многочлена первой степени и показательной функции, а также коэффициент в показателе степени совпадает с одни из корней характеристического уравнения, следовательно, необходимо в частное решение добавить множитель х и частное решение будт иметь вид

y*= x(Ax+B)e^-4x=(Ax²+Bx)e^-4x.

Вычислим производные функции у*

y*'= 2Axe^-4x-4e^-4x(Ax²+Bx) = (-4Ax²+2Ax-4Bx+B)e^-4x

y*" = (-8Ax+2A-4B) e^-4x-4e^-4x(-4Ax²+2Ax -4Bx+B)=

= (16Ax²-16Ax +16Bx+2A – 8B)e^-4x.

Подставим найденные производные в неоднородное уравнение

(16Ax²-16Ax +16Bx+2A – 8B)e^-4x+4(-4Ax²+2Ax-4Bx+B)e^-4x=-2xe^-4x

(16Ax²-16Ax +16Bx+2A – 8B+16Ax²+8Ax-16Bx+4B)e^-4x=-2xe^-4x.

Приведем подобные члены и сократим равенство на е^-4х

-8Ax+2A -4B =-2x.

Приравняем коэффициенты левой и правой части равенства, стоящие перед х в одинаковой степени, получим систему уравнений, решив которую найдем значения неопределенных коэффициентов А и В:

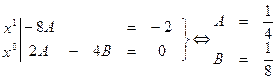
Получили частное решение неоднородного уравнения

y*=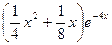

Теперь можно записать общее решение данного неоднородного уравнения

y = С₁ +C₂e^-4х+ .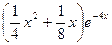

Пример 10.13. Найти общее решение дифференциального уравнения

y"+4y=3xcosx.

Решение. Общее решение неоднородного уравнения равно сумме общего решения 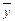однородного уравнения и какого-либо частного решения у* неоднородного уравнения:

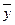у = + у*.

Найдем общее решение однородного уравнения

y"+4y=0.

Составим характеристическое уравнение и решим его

k² + 4 = 0, k_1,2=±2i (α=0, β=2)

Общее решение однородного уравнения имеет вид

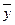= С₁cos2x +C₂ sin2x.

Перейдем к отысканию частного решения у* данного уравнения. Здесь правая часть неоднородного уравнения f(x)=3xcosx содержит произведение многочлена первой степени и тригонометрической функции (α =0, β =1), коэффициенты в правой части неоднородного уравнения не совпадают с корнями характеристического уравнения и частное решение будет иметь вид

y*= (Ax+B)cosx+(Cx+D)sinx,

где A,B,C,D – неопределенные коэффициенты.

Вычислим производные функции у*:

y*'=Acosx - (Ax+B)sinx + Csinx + (Cx+D)cosx=(Cx + D + A)cosx +

+(-Ax +C - B)sinx

y*" =Ccosx - (Cx + D +A)sinx – Asinx+(-Ax+C-B)cosx=(-Ax + 2C – B)cosx + +(-Cx – 2A – D)sinx

Подставим найденные производные в неоднородное уравнение, приведем подобные члены и сгруппируем члены при cosx и sinx

(3Ax + 3B + 2C)cosx + (3Cx + 3D - 2A)sinx = 3xcosx

3Axcosx + 3Cxsinx + (3B+2C)cosx + (3D-2A)sinx = 3xcosx

Приравняем коэффициенты левой и правой части равенства, стоящие перед xcosx, xsinx, cosx и sinx получим систему уравнений, решив которую найдем значения неопределенных коэффициентов A,B,C,D:

Таким образом, частное решение имеет вид

y*=xcosx+ sinx.

Окончательно получаем общее решение неоднородного дифференциального уравнения

у = С₁cos2x +C₂ sin2x+ xcosx+ sinx.

Поиск по сайту: