 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема 2. Транспортная задача
Задача 2. На трех базах 
, 
, 
находится однородный груз в количестве 200, 200 и 100 т. Этот груз необходимо развезти пяти потребителям 
, 
, 
, 
, 
, заявки которых на данный груз составляют 70, 80, 150, 110 и 90 т соответственно. Стоимость перевозок пропорциональна количеству перевозимого груза. Стоимость 
перевозки единицы груза (тариф) с базы 
потребителю 
известна и матрица тарифов имеет вид:
.
Спланировать перевозки так, чтобы их общая стоимость была минимальной.
Решение. По исходным данным задачи составим распределительную таблицу:
  ПН
ПО
|
|
|
|
|
| Запасы а i |
|
| ||||||
|
| ||||||
|
| ||||||
| Заявки b j |  500
|
Строки таблицы соответствуют базам (пунктам отправления, ПО), а столбцы – потребителям (пунктам назначения, ПН). Каждая клетка на пересечении некоторой строки и какого-либо столбца соответствует одному маршруту перевозок (например, клетка на пересечении и , которую будем обозначать (2,3), отвечает маршруту перевозки с базы потребителю ). Соответствующие тарифы перевозок указаны в правом верхнем углу каждой клетки.
Так как в данной задаче выполняются условия баланса: 
,
то имеем закрытую модель транспортной задачи, и можно непосредственно приступать к её решению. Решение транспортной задачи проводится в два этапа. На первом этапе находится первоначальный опорный план перевозок. На втором этапе на основе найденного опорного плана методом потенциалов определяется оптимальный план. Первоначальный опорный план можно найти разными методами, из которых рассмотрим два: метод северо-западного угла и метод минимальной стоимости. Затем из найденных планов выберем лучший. Его, в случае необходимости, и подвергнем процедуре дальнейшей оптимизации методом потенциалов. Пусть 
- количество перевозимого груза из пункта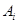 
в пункт 
.
Рассмотрим вначале метод северо-западного угла, или диагональный метод. В этом методе заполнение транспортной таблицы всегда начинается с клетки (1,1), т.е. “северо-западного угла” таблицы. Далее, заполнение идет слева направо и сверху вниз “вокруг” диагонали таблицы и всегда заканчивается в правом нижнем углу (клетка (3,5)). В каждой клетке объем перевозки определяется как наименьшее значение из двух чисел: запаса или его остатка на базе и заявки потребителя или её неисполненной части. Отсюда:
= min { 
, 
} = {200; 70} = 70.
Таким образом, заявка первого потребителя выполняется в полном объеме. Поэтому остальные клетки первого столбца не могут больше заполняться перевозками с других баз и должны оставаться пустыми. Чтобы не путать их с теми клетками, которые будут ещё заполняться перевозками, эти клетки помечают каким-нибудь символом, например, в них ставят точки. Далее наступает очередь второго заказчика, который со своей заявкой обращается на первую базу, где еще остался товар:
= min {200 - 70; 80} = {130; 80} = 80.
Он также полностью удовлетворяет свою заявку, и остальные клетки второго столбца также метятся точками. Теперь на первой базе осталось только 50 т груза. Поэтому третий заказчик получит только эти 50 т, хотя ему требуется 150 т:
= min {200 – 70 – 80; 150} = 50.
Поскольку на первой базе больше не осталось товара, то остальные клетки первой строки заполняются точками. Неисполненную часть своей заявки второй заказчик получит на второй базе:
= min {200; 150 – 50} = 100.
Далее аналогичный процесс повторяется для остальных потребителей, в результате получаем следующий опорный план перевозок:
| ПН
ПО
|
|
|
|
|
| а i |
|
| . | . | ||||
|
| . | . | . | |||
|
| . | . | . | |||
| b j |
Если в опорном плане число заполненных перевозками клеток равно m +n – 1, где m – число баз, n - число потребителей, то план является невырожденным. Если таких клеток меньше, чем m +n – 1, то план называется вырожденным. В нашем случае план является невырожденным, так как число заполненных клеток равно 7 и 
3+5-1=7.
Осталось подсчитать общую стоимость перевозок. Она складывается из произведений объемов перевозок и тарифов по всем заполненным клеткам, т.е.
= 70 × 4 + 80 × 11 + 50 × 5 + 100 × 9 + 100 × 13 + 10 × 7 + 90 × 20 = 5530.
При распределении грузов в рассмотренном методе совсем не учитывается стоимость перевозок. Поэтому, как правило, метод северо-западного угла дает опорный план, далекий от оптимального.
Построим опорный план вторым методом – методом минимальной стоимости (или минимального элемента), который находится уже с учетом тарифов. Сначала в таблице находят клетку с наименьшим тарифом. Если таких клеток несколько, то выбирают любую из них. В эту клетку помещают максимально возможную перевозку, а затем отмечают точками клетки, ставшие ненужными. Далее в оставшейся незаполненной части таблицы процесс повторяется, пока вся таблица не будет заполнена перевозками или точками.
В данном случае клетка (1, 1) имеет наименьший тариф 
. С неё и начинаем распределение грузов: х 11 = min {200; 70} = 70.
Исключаем из рассмотрения клетки первого столбца и повторяем процесс в оставшейся части таблицы. Запишем последовательность заполнения клеток:
х 14 = min {200 - 70; 110} = 110; х 32 = min {100; 80} = 80; х 13 = min {200 – 70 – 110; 150} = 20;
х 23 = min {200; 150 - 20} = 130; х 25 = min {200 - 130; 90} = 70; х 35 = 20.
Получаем следующий опорный план:
| ПН
ПО
| В 1 | В 2 | В 3 | В 4 | В 5 | b j |
| А 1 | . | . | ||||
| А 2 | . | . | . | |||
| А 3 | . | . | . | |||
| а i |
Здесь получены семь ненулевых перевозок, поэтому план также невырожденный. Подсчитаем его стоимость:
= 4 × 70 + 6 × 20 + 5 × 110 + 9 × 130 + 10 × 70 + 5 × 80 + 20 × 20 = 3620.
Как видим, этот опорный план дешевле первого. Поэтому его берем в качестве исходного для дальнейшей оптимизации по методу потенциалов.
Основой метода потенциалов является теорема о потенциалах:
план 
транспортной задачи является оптимальным тогда и только тогда, когда существуют такие числа ui (i = 
), vj (j = 
), называемые соответственно потенциалами поставщиков и потребителей, для которых выполняются соотношения:
(1)
Как видим из системы (1), уравнения записываются для заполненных клеток, а неравенства – для свободных клеток. В правых частях неравенств выражения (1) стоят тарифы перевозок в соответствующих клетках.
На этой теореме основывается алгоритм метода потенциалов для оптимизации планов транспортной задачи. Рассмотрим его по шагам.
Шаг 1. Определение потенциалов поставщиков и потребителей.
На этом шаге для определения потенциалов составляется система уравнений, получаемая из выражения (1) для заполненных клеток (
). За исходный возьмем последний опорный план. Для удобства распределительную таблицу представляют в упрощенном виде, помещая в заголовочных клетках таблицы только значения потенциалов:
| ПН
ПО
| v 1=4 | v 2=-8 | v 3=6 | v 4=5 | v 5=7 |
| u 1=0 | 19 11 . |
  20 +
|
 110-
| 8 15 . | |
| u 2=3 | 1 8 . | 12 7 . |
 130-
| 6 13 . |
 70 +
|
| u 3=13 | -7 10 . | -7 12 . | -11 7
 +.
| 20 - |
Тогда получаем следующую систему линейных уравнений:
Заметим, что в этой системе 8 неизвестных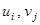 
, так как m + n= 3 + 5. Однако уравнений всего только 7, поскольку в невырожденном опорном плане 7= 
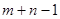заполненных клеток. Для однозначного решения не хватает одного уравнения. В этом случае один из потенциалов, например, и 1 (целесообразнее выбирать тот, который присутствует в большем числе уравнений) приравнивают некоторому постоянному числу, например, нулю:
=0.
Это и будет недостающим уравнением в системе. Теперь систему можно легко решить, имея в виду, что все уравнения линейны и состоят только из двух неизвестных. Результаты решения записаны в заголовочных клетках таблицы.
Потенциалы можно определять и непосредственно по таблице, используя занятые клетки и заданное значение одного из потенциалов.
Сделаем замечание для случая, когда исходный опорный план получается вырожденным. Это возникает тогда, когда при заполнении очередной клетки перевозкой 
одновременно исчерпываются запасы груза на базе и удовлетворяется заявка потребителя. Для получения невырожденного плана вместо одной из точек либо в строке, либо в столбце выставляется ноль, называемый базисным. В последующем эта клетка с базисным нулем считается заполненной наряду с положительными перевозками. Рекомендуется базисный ноль проставлять в клетке с наименьшим тарифом.
Такая модификация опорного плана не влияет на его стоимость, поскольку нулевые перевозки имеют нулевые стоимости. Базисные нули ставят не произвольно, а по некоторому правилу, о котором будет сказано ниже.
Шаг 2. Проверка оптимальностиопорного плана.
На этом шаге проверяем выполнение неравенств (1) для свободных клеток. Введем в рассмотрение величины:
, 
; 
, (2)
которые называют оценками свободных клеток.
Если все оценки 
неотрицательны, то условия (1) теоремы о потенциалах выполняются и опорный план является оптимальным, и на этом вычислительный процесс заканчивается. В противном случае план перевозок не оптимален и его требуется улучшить. Отметим, что по условию (1) оценки заполненных клеток равны нулю. Подсчитаем оценки для свободных клеток:
= 11 – (0 - 8) = 19 ³ 0, 
= 15 – (0 +7) = 8 ³ 0, 
= 8 – (3 + 4) = 1 ³ 0,
= 7 – (3 - 8) = 12 ³ 0, 
= 13 – (3 + 5) = 5 ³ 0, 
= 10 – (13 + 4) = -7< 0,
= 12 – (13+ 6) = - 7 < 0, 
= 7 – (13 +5) = -11 < 0.
Вычисленные значения оценок помещаем в левом верхнем углу свободных клеток распределительной таблицы. Оценки 
оказались отрицательными, и рассматриваемый опорный план не является оптимальным. Он нуждается в изменении, которое проведем на следующем этапе.
Шаг 3.Пересчет по циклу.
Для пересчета плана выбирается клетка, в которой оказалась наименьшая отрицательная оценка. Таких клеток может оказаться несколько. В этом случае для пересчета выбирается любая из них. Переход от одного допустимого плана к другому осуществляется путем переноса части груза по циклу.
Циклом в распределительной таблице называется замкнутая ломаная с прямыми углами, проведенная через клетки таблицы так, что каждая пара угловых соседних клеток ломаной расположены либо в одной строке, либо в одном столбце. Угловые клетки цикла, кроме одной (для которой организуется пересчет, т.е. с отрицательной оценкой), являются заполненными.
Цикл всегда существует и является единственным.
 |
Циклы могут иметь различную конфигурацию, например:
В последнем случае место пересечения двух линий цикла не входит в сам цикл, поскольку в вершинах цикла совершается поворот на 90 0. Заполненные клетки, через которые проходит прямая линия цикла, также не принадлежат циклу.
Каждой вершине цикла присваивается знак плюс или минус. При этом начальная клетка цикла, котороя является свободной, помечается знаком плюс. Остальные вершинные клетки имеют чередующиеся знаки. Поскольку очевидно, что любой цикл имеет четное число вершин, то количество отрицательных и положительных вершин всегда будет одинаковым.
В данном случае цикл пройдет через клетки (3,4), (1,4), (1,3), (2,3),(2,5),(3,5),(3,4). В таблице цикл обозначен пунктирными линиями.
В опорном плане нельзя построить замкнутый цикл, в который входили бы только заполненные клетки. Это привело бы к противоречивой системе уравнений для потенциалов. Данное замечание подсказывает правило, по которому в вырожденный опорный план должны быть помещены базисные нули: их нельзя располагать в клетках, которые могут создать замкнутый цикл только из заполненных клеток.
Теперь вернемся к построенному нами циклу. Из всех вершин цикла, помеченных знаком минус, выбираем наименьшее значение перевозок:
.
Далее на значение 
уменьшаем перевозки в вершинах цикла, помеченных знаком минус, а во всех положительных вершинах значения перевозок увеличиваем на эту же величину. Остальные заполненные клетки, не вошедшие в цикл, не изменяются. Поскольку в цикле чётное число вершин, то в пределах цикла общий объём перевозок не изменится, что не приведет к нарушению баланса между запасами и заявками. Пересчитанная таблица выглядит так:
| ПН ПО | v 1=4 | v 2=3 | v 3=6 | v 4=5 | v 5=7 |
| u 1=0 | 8 11 . | 8 15 . | |||
| u 2=3 | 1 8 . | 1 7 . | 5 13 . | ||
| u 3=2 | 4 10 . | 4 12 . | 11 20 |
Найдем стоимость нового плана:
= 4 × 70 + 6 × 40 + 5 × 90 + 9 × 110 + 10 × 90 + 5 × 80 + 7 × 20 = 3400.
Как видим, стоимость перевозок уменьшилась. Для нового опорного плана повторим вычисления по описанным шагам.
Система уравнений для определения потенциалов здесь почти не отличается от предыдущей, кроме одного уравнения. Это связано с тем, что свободная клетка (3, 4) стала заполненной перевозкой в 20 ед. груза, а клетка (3,5) стала свободной. Фактически здесь идет речь о преобразовании однократного замещения, которое имело место в симплекс-методе. Соответственно последнее уравнение для потенциалов заменяется другим:
.
Решаем эту систему аналогично предыдущей и результаты вычислений помещаем в заголовочные клетки последней таблицы.
Далее по формуле (2) находим оценки свободных клеток, которые помещаем в левом верхнем углу этих клеток.
Поскольку все оценки свободных клеток оказались неотрицательными, то полученный план является оптимальным. В противном случае пришлось бы продолжать вычислительный процесс до получения оптимального плана.
Запишем оптимальное решение транспортной задачи:
,
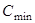=3400.
Поиск по сайту: