АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Численные методы первого порядка (градиентные)

Читайте также:
  1. I Классификация кривых второго порядка
  2. II ОБЩИЕ НАЧАЛА ПУБЛИЧНО-ПРАВОВОГО ПОРЯДКА
  3. II. Методы непрямого остеосинтеза.
  4. II. Рыночные методы.
  5. II. САКРАЛЬНАЯ ГЕОМЕТРИЯ: МЕТАФОРА УНИВЕРСАЛЬНОГО ПОРЯДКА
  6. III. Методы искусственной физико-химической детоксикации.
  7. III. Параметрические методы.
  8. IV. Современные методы синтеза неорганических материалов с заданной структурой
  9. IV.1. Общие начала частной правозащиты и судебного порядка
  10. V2: ДЕ 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка
  11. V2: ДЕ 54 - Дифференциальные уравнения, допускающие понижение порядка
  12. V2: ДЕ 6 - Линейные отображения. Определители второго порядка

3.3.3.1. Постановка задачи.

Понятие градиента и его геометрическая интерпретация.

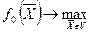, V: , где 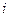= 1,2…n.

Градиентом функции называется вектор в пространстве варьируемых переменных 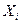, направление которого в данной точке соответствует наискорейшему возрастанию функции.

Построение вектора градиента производится по его проекциям на оси координат, которые равны частным производным целевой функции по соответствующим переменным.

, в max

В двумерном случае в любой точке на плоскости переменных градиент направлен перпендикулярно касательной, проведённой к линии равного уровня в данной точке (рис. 3.8).


Рис. 3.8


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)