Линейного программирования

Рассмотрим следующую основную задачу линейного программирования. Пусть заданы ограничения:

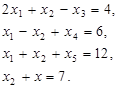
и функция цели

. (10)

Требуется среди всех неотрицательных решений системы линейных уравнений найти такое, при котором функция F принимает наибольшее значение. Система является неопределенной и степень неопределенности p=6-4=2.

Применим следующий метод. Выберем в качестве базисных неизвестных неизвестные х₃; х₄; х₅; х₆, а в качестве свободных неизвестных – неизвестные х₁ и х₂. Перенося члены уравнений со свободными неизвестными в правые части и умножая первое уравнение на (-1), получаем общее решение системы:

(11)

Она имеет бесчисленное множество решений. Однако надо рассмотреть только те, которые имеют неотрицательные решения этой системы. Поэтому дополним эти уравнения условиями неотрицательностии перепишем:

Множество решений системы неравенств называют областью определения допустимых решений или просто областью допустимых решений данной ЗЛП.

Установим геометрический смысл неравенств, т.е. установим, что представляет собой геометрическая область допустимых решений рассматриваемой ЗЛП. Для этого введем систему координат Х₁ – 0 – Х₂. Полагая, что в неравенствах крайний случай – знак равенства, получаем следующие уравнения:

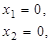
Этим уравнениям геометрически соответствуют прямые на плоскости Х₁ – 0 – Х₂ , рис.1. Каждая из прямых делит всю плоскость Х₁ – 0 – Х₂ на две полуплоскости: координаты точек одной из них удовлетворяют соответствующему неравенству (эти направления указаны стрелками на линиях), а другой – не удовлетворяют. Обычно эту оценку очень просто осуществить подстановкой в ограничения–неравенства нулевых значений входящих в них переменных (это начало координат) и дать оценку неравенству. Если нулевые значения переменных удовлетворяют неравенству, то ориентационные стрелки на соответствующих разграничительных линиях направляют в сторону начала координатной системы (и наоборот).

Рис.1. Графическая интерпретация решения задачи

линейного программирования

Очевидно, что область допустимых решений будет лежать внутри замкнутого многоугольника. Это многоугольник допустимых решений основной ЗЛП. Для рассматриваемого случая – многоугольник MNPKQL. Такой многоугольник всегда выпуклый.

Координаты любой точки, лежащей как внутри этой области, так и на ее сторонах, будут удовлетворять условиям ограничений ЗЛП. Но задача заключается в том, чтобы среди этого бесчисленного множества возможных решений, лежащих внутри очерченной области, найти такое, которое было бы оптимально, т.е. функция цели принимала наибольшее значение. Выразим функцию цели через свободные неизвестные х₁ и х₂ , для чего в (10) подставим равенства (11) и в результате получим функцию:

. (12)

Очевидно, эта функция аргументов х₁ и х₂ в каждой точке многоугольника допустимых решений принимает определенное значение, и в какой-то, по крайней мере одной его точке, она примет наибольшее значение. Найдем эту точку многоугольника, для чего введем в рассмотрение вспомогательную функцию:

; т.е. .

Функция F₀ отличается от первичной лишь на постоянную, поэтому они будут иметь один экстремум, т.е. F₀ принимает наибольшее значение в той же точке многоугольника, что и функция F. Воспользуемся известной геометрической трактовкой функции двух переменных – линиями уровня. Линии уровня – это геометрическое место точек, в которых функция принимает одно и то же значение. Пусть С - некоторое произвольное значение, принимаемое функцией F₀ . Тогда уравнение линии уровня, соответствующей этому значению, имеет вид:

или относительно х₂ :

. (13)

Любая линия, имеющая коэффициент угла наклона k=(-1/2), будет отвечать уравнению (13). Но через каждую точку плоскости может проходить только одна линия уровня функции и среди них найдется такая, для которой будет соответствовать конкретное значение С (или, что одно и то же, F₀). Для другой точки, через которую пройдет линия уровней (т.е. в данном случае прямая с постоянным угловым коэффициентом k=(-1/2), будет другое значение F₀. Учитывая это, найдем среди всех точек многоугольника допустимых решений ту, через которую проходит линия уровня функции F₀ с ее наибольшим значением. Эта точка будет соответствовать оптимальному решению рассматриваемой ЗЛП.

Построим линию уровня, предполагая, что F₀=С=0. Это имеет место при х₁=0 и х₂=0, причем линия должна иметь угловой коэффициент k=(-1/2). На рис.1 это линия ab, проведенная через начало координат. Стрелкой указано направление, в котором будут располагаться линии уровня с более высокими значениями функции цели. Действительно, исходя из структуры функции F (уравнение 12), видно, что чем больше будут принимать значение величины х₁ и х₂, тем больше будет функция цели F. Поэтому естественно линию функции F₀ надо перемещать вверх и вправо, и чем дальше она будет расположена от начала координат, тем больше значение функции цели. Тогда геометрически эта задача решается просто: необходимо перемещать линию уровней F₀=0 параллельно самой себе и определить крайнюю точку контакта этой линии и многоугольника области допустимых решений. В данном случае этому условию отвечает точка М, координаты которой получим, решая систему уравнений

,

.

Они равны х₁=5, х₂=7. Тогда нетрудно найти и остальные независимые величины: х₃=13; х₄=8; х₅=0; х₆=0, а соответственно и наибольшее значение функции цели F_мах= - 16.

Таким образом, основная ЗЛП с помощью геометрических построений решена. Очевидно, аналогичными геометрическими построениями может быть решена и любая другая основная ЗЛП, у которой ограничения имеют степень неопределенности р=2.

Можно сформулировать признаки, справедливые для общего случая основной задачи ЛП.

1. Если основная ЗЛП имеет допустимые решения, то область этих решений геометрически представляет собой замкнутое выпуклое многогранное тело. Геометрическую наглядность это тело имеет только в случаях р=2 (многоугольник) и р=3 (многогранник). Для случаев р>3 наглядное представление об этом теле теряется, но, несмотря на это, геометрическая трактовка области допустимых решений сохраняется, и в этих случаях говорят о так называемых гипермногогранниках, размерность которых равна р. Область допустимых решений всегда выпуклая, замкнутая, имеет конечное число вершин (крайних точек), но может быть неограниченной (т.е.иметь бесконечно удаленные точки).

2. Решение, соответствующее одной из вершин многогранника допустимых решений, называется опорным решением основной ЗЛП (или опорный план). В каждом опорном решении не менее р неизвестных имеют нулевое значение.

3. Оптимальное решение, если оно существует, всегда достигается по крайней мере в одной из вершин многогранника допустимых решений, т.е. оптимальное решение ЗЛП всегда совпадает по крайней мере с одним из ее опорных решений. Возможен случай, когда оптимальное решение достигается на всем ребре или даже на всей грани многогранника. В таких случаях ЗЛП имеет единственное (и оптимальное) значение функции цели, но достигается оно в бесчисленном множестве оптимальных планов (решений).

Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция F принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. Рис.2а характеризует такой случай, когда целевая функция принимает экстремальное значение в единственной точке А. Из рис2b видно, что экстремальное значение целевая функция принимает в любой точке отрезка АВ. На рис.2с изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений и решения задача не имеет, равно как и в

Рис.2. Типы областей допустимых решений ЗЛП

случае, представленном рис.2d, когда система ограничений задачи несовместна.

Поиск по сайту: