Графический метод

Итак, нахождение решения ЗЛП на основе ее геометрической интерпретации возможно, если она записана в виде, имеющем степень неопределенности р=2 (т.е. все переменные и функция цели могут быть выражены через две свободные) и процесс включает следующие этапы:

1.Строят прямые, уравнения которых получают в результате замены в ограничениях знаков неравенств на знаки точных равенств.

2. Находят полуплоскости, отвечающие требованиям каждого из ограничений задачи.

3. Находят многоугольник решений (область допустимых решений).

4. На основании функции цели находят уравнение функции F₀ и строят линию уровней, проходящую через начало координатной системы и отвечающую значению F₀=0.

5. Перемещают линию уровней в направлении многоугольника области допустимых решений параллельно самой себе, в результате находят точку (точки), в которой функция цели принимает заданное экстремальное значение.

6. Определяют координаты точки экстремума (значений свободных переменных), по ним вычисляют параметры всего оптимального плана и затем экстремальное значение функции цели.

Если после выполнения процедуры по п.3 получают незамкнутый многоугольник, то такая задача решения не имеет.

Задача 4. Найти максимальное значение функции

при условиях

,

, (14)

,

.

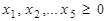Р е ш е н и е. Задача записана в основной форме, имеет пять переменных и в таком виде графически не может быть решена. Однако ее можно записать в стандартной форме и тем самым снизить количество неизвестных. Действительно, записав ограничения-равенства (14) относительно переменных х₃, х₄, х₅ и переходя к неравенствам, перепишем ЗЛП следующим образом: найти максимальное значение функции при ограничениях

,

, (15)

,

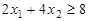х₁, х₂,…х₅ ≥ 0.

Теперь она записана в стандартной форме, имеет степень неопределенности р=2 и может быть решена графическим методом.

В двухкоординатной системе (рис.3) проведем следующие линии:

1) линию m-n, которая отвечает первому неравенству в системе (15);

2) линию p-q, которая отвечает второму неравенству в системе (15);

3) линию r-s, которая отвечает третьему неравенству в системе (15).

Затем для каждой линии, положив х₁=х₂=0 (начало координат) в системе неравенств (15), определим те полуплоскости, которые отвечают смыслу имеющихся ограничений в задаче. Добавим к уже построенным линиям ограничения неотрицательности по х₁, х₂.

В результате таких построений получили область допустимых решений – четырехсторонний многоугольник ABCD. Соответственно, записанная в стандартной форме, наша задача будет иметь четыре опорных плана. Для нахождения оптимального плана построим линию уровней, для чего приравняем нулю функцию цели и найдем уравнение линии уровней:

.

Рис. 3. Графическая интерпретация задачи 4

Ее легко провести, положив в этом уравнении х₁=0 и х₁=3. Соответственно получим два значения другой координаты: х₂=0 и х₂= -2. По этим двум точкам проведем линию a-b, которая отвечает значению функции цели F=0. Так как в уравнение функции цели положительные переменные входят со знаком плюс, то будем искать такое положение линии уровней, при котором переменные х₁, х₂ примут максимальное значение. Перемещая линию уровней параллельно самой себе в направлении области допустимых решений, определим такую точку. Ею будет вершина С многоугольника ABCD. Для получения оптимального плана и соответственно значения функции цели надо найти координаты этой точки. Так как она является точкой пересечения двух линий mn и pq, то, записав их уравнения в систему

,

.

и решив ее, получим х₁^*=3, х₂^*=4.

Подставляя найденные значения х₁*, х₂* в начальные уравнения-ограничения (14), получим: х₃=0, х₄=0, х₅=14. Следовательно, оптимальным планом рассматриваемой задачи является Х^*=(3; 4; 0; 0; 14). При этом плане значение функции цели есть F_max=18.

Если бы необходимо было найти минимальное значение функции цели, то очевидно, что оно будет определяться планом, параметры которого соответствуют координатам точки В у многоугольника области допустимых решений. Именно в этой точке линия уровней впервые коснется этой области, а переменные х₁, х₂ будут иметь минимальные из возможных значения.

Следует обратить еще на одну особенность в геометрической интерпретации ЗЛП. Линии, ограничивающие область допустимых решений, пересекаясь, позволяют рассчитать параметры какого-либо опорного плана. Но каждая из линий построена на основании того, что соответствующее уравнение ограничений получают приравниванием нулю одной из входящих в него переменных. Это означает, что в каждом опорном плане несколько переменных должны быть равны нулю. Их количество всегда равно степени неопределенности задачи или, что одно и то же – количеству пересекающихся в вершине многоугольника (многогранника) ограничительных линий (ребер). В рассмотренной выше задаче оно было равно двум. И действительно

1) в точке А х₂=х₅=0,

2) в точке В х₁=х₄=0,

3) в точке С х₃=х₄=0,

4) в точке D х₂=х₃=0.

В задачах, решаемых графическим методом, степень неопределенности, а соответственно и количество переменных, принимающих нулевое значение, всегда равно двум.

При графическом методе решения ЗЛП следует обратить еще на одно обязательное условие – функция цели должна содержать переменные только с одинаковыми знаками. Если это правило будет нарушено, то появляется неопределенность в направлении перемещения линии уровней для достижения заданного оптимума. В этом случае надо перейти к другой паре свободных переменных.

Поиск по сайту: