Леммы и теоремы двойственности

Если число переменных в прямой и двойственной задачах, образующих данную пару, равно двум, то, используя геометрическую интерпретацию ЗЛП, можно легко найти решение данной пары задач. При этом возможны один из трех взаимоисключающих случаев:

1) обе задачи имеют планы;

2) планы имеет только одна задача;

3) для каждой задачи двойственной пары множество планов пусто.

З а д а ч а 9. Для задачи, состоящей в определении максимального значения функции при условиях

,

,

,

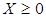составить двойственную задачу и найти решение обеих задач.

Р е ш е н и е. Двойственной задачей по отношению к прямой является задача, состоящая в определении минимального значения функции

при условиях

,

,

.

Как в исходной, так и в двойственной задаче, число неизвестных равно двум. Следовательно, их решение можно найти, используя геометрическую интерпретацию ЗЛП.

На рис.5 представлено решение прямой задачи. Область допустимых решений - это неправильный четырехугольник, ограниченный осями координат в соответствии с неотрицательностью переменных и двумя линиями, уравнения которых есть крайний случай ограничений-неравенств. Уравнение линии уровней

Рис.5. Геометрическая трактовка прямой задачи

позволяет определить, что координаты одной из вершин четырехугольника (точка А) составят оптимальный план задачи. Для его нахождения решаем систему линейных уравнений:

,

.

Решение дает оптимальный план , и соответственно функция цели принимает значение .

Построим теперь геометрическую интерпретацию двойственной задачи. Она представлена на рис.6. Видно, что область допустимых решений для рассматриваемой двойственной задачи не ограничена сверху. Тем не менее, при условии нахождения плана, при котором функция цели принимает минимальное значение (следовательно, переменные y₁, y₂ также должны принять минимальное значение) и линии уровней

решение будет лежать в точке В, т.е. оптимальный план для двойственной задачи найдем как решение системы линейных уравнений:

,

.

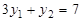Рис. 6. Геометрическая трактовка двойственной задачи

Он запишется , а функция цели примет значение , т.е. при различии в содержании оптимальных планов значения функции цели одинаковы. При этом для прямой задачи область допустимых решений дает значение функции цели 46 и менее, а для двойственной задачи область допустимых решений дает значение функции цели 46 и более (причем без ограничений).

Рассмотренный пример позволяет сделать ряд существенных наблюдений, характеризующих двойственную пару:

- прямая задача имела типичную, полностью определенную область допус-

тимых решений с оптимальным планом;

- у двойственной задачи область допустимых решений не была ограничена

сверху, тем не менее оптимальный план двойственная задача имела;

- при наличии оптимальных планов двойственная пара имеет одно значение

функции цели, причем экстремум функции цели в точке оптимума прямо

противоположен для прямой и двойственной задач;

- при равенстве значений функции цели физическая сущность функции цели

для этих задач различна.

На основании вышеприведенной информации и не останавливаясь на теоретических выкладках, приведем некоторые из основных положений теории двойственности.

Л е м м а 1. Если Х – некоторый план прямой задачи (записанной в основной форме), а Y – произвольный план двойственной задачи, то значения функции цели прямой задачи при плане Х всегда не превосходит значения функции цели двойственной задачи при плане Y, т.е. .

Л е м м а 2. Если для некоторых планов Х^* и Y^* прямой и двойственной задач, то Х^* - оптимальный план прямой задачи, а Y^* - оптимальный план двойственной задачи.

П е р в а я т е о р е м а д в о й с т в е н н о с т и. Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций этих задач при их оптимальных планах равны между собой, т.е. .

Поиск по сайту: