Метод штрафных функций

Задачу динамического программирования, содержащую ограничения в виде неравенств, можно решать различными методами. Один из методов решения ЗДП основывается на принципе «проб и ошибок» - метод штрафных функций. Его идея заключается в следующем.

Рассмотрим задачу определения максимального значения вогнутой функции при условиях (, , 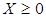где - выпуклые функции.

Вместо того чтобы непосредственно решать эту задачу, находят максимальное значение функции

,

которая является суммой целевой функции задачи и некоторой функции Н, определяемой системой ограничений и называемой штрафной функцией. Штрафную функцию можно построить различными способами, но наиболее часто она имеет вид:

,

где >0 - некоторые постоянные числа, представляющие собой весовые коэффициенты

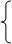0, если ,

α_i, если .

Используя штрафную функцию, последовательно переходят от одной точки к другой до тех пор, пока не получат приемлемое решение. Таковым будет очередной опорный план, который удовлетворит ранее приведенному условию, а именно .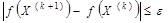

Процесс итерации осуществляют по рекуррентной формуле:

, (30)

где λ – шаг вычислений (см. метод наискорейшего спуска).

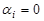Из формулы (30) следует, что если предыдущая точка находится в ОДР исходной задачи (а это означает и соответственно ), то второе слагаемое в квадратных скобках равно нулю и переход к последующей точке определяется только градиентом целевой функции. Иначе, если предыдущая точка находится в ОДР, то переход к последующей выполняется по схеме наискорейшего спуска (в пределах положительных значений переменных). Если же указанная точка не принадлежит ОДР, то за счет подключаемого слагаемого и соответственно штрафной функции на последующих итерациях достигается возвращение точки в ОДР. Следовательно, назначение штрафной функции – вернуть текущую контрольную точку итерации в ОДР.

Шаг вычислений подбирается так же, как и при методе крутого спуска. В процессе вычислений шаг может оставаться постоянным, но при очевидном приближении к решению шаг нужно уменьшать. Что касается коэффициентов α_i, их находят в результате компромиссного выбора из n уравнений, описывающих параметры очередной точки итерации (см. задачу ниже). Следовательно, теоретически для каждой исследуемой точки эти коэффициенты могут иметь индивидуальное значение. Обычно их выбирают таким образом, чтобы исследуемая точка не уходила далеко от границы ОДР. Чем меньше α_i, тем быстрее находится приемлемое решение, однако точность его определения снижается. Поэтому итерационный процесс обычно начинают при сравнительно малых значениях α_i и, продолжая его, эти значения постепенно увеличивают.

Итак, процесс нахождения решения задачи выпуклого программирования методом штрафных функций включает следующие этапы:

1) определяют исходное допустимое решение;

2) назначают шаг вычислений;

3) находят по всем переменным частные производные от целевой функции

и функций, определяющих ОДР;

4) по рекуррентной формуле находят координаты точки, определяющей

возможное новое решение задачи;

5) проверяют, удовлетворяют ли координаты найденной точки системе

ограничений задачи и условию точности:

- если выполняются оба условия, завершают процесс вычислений;

- если требуемая точность не достигнута, а опорный план находится в

ОДР, то переходят к п.4;

- если требуемая точность не достигнута и опорный план находится вне

ОДР, то устанавливают значения весовых коэффициентов и переходят

к п.4.

З а д а ч а 29. Найти максимальное значение функции

при условиях ,

.

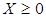Точность вычислений по функционалу обеспечить не ниже 1%.

Р е ш е н и е. Целевая функция представляет собой вогнутый параболоид с вершиной в начале координат, т.е. она имеет отрицательно-определенную квадратичную форму. В то же время область допустимых решений - это геометрическое место точек, ограниченное объемом цилиндра с вертикальной осью симметрии Е, имеющей координаты , . Радиус цилиндра ОДР равен . Очевидно, решение находится на части поверхности отклика функции цели (т.е. параболоида), отсекаемой вертикально расположенным цилиндром ограничений, рис.21.

Линиями уровня будут окружности переменного диаметра, которые являются следами пересечения горизонтальных плоскостей с поверхностью отклика функции цели – параболоидом. На рис.21 они показаны в виде дуг для различных значений функции f. Так как вся функция цели находится в области отрицательных значений, то условию максимума будет отвечать точка первого контакта линии уровня с поверхностью цилиндра функции ограничений. Это должна быть точка D, рис.20. Найдем ее координаты, применив для решения задачи метод штрафных функций.

Начнем с выбора первичной точки. Ее следует выбирать в ОДР. Теоретически безошибочно можно было бы взять координаты центра ОДР, т.е. координаты точки Е. Но мы поступим иначе. Выберем начальную точку с координатами , т.е. .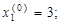

Рис.21. Геометрическая трактовка задачи 29

Вычислим дифференциал функции цели и частные производные функции ограничений:

, ,

, .

Удостоверимся в том, что начальная точка действительно находится в ОДР. Для этого выполним следующие расчеты:

,

следовательно, выбранная точка принадлежит ОДР. Это означает, при переходе к очередной точке пользуемся рекуррентной формулой метода наискорейшего спуска. Примем величину шага вычислений . Тогда:

1 и т е р а ц и я ,

.

Итак, имеем очередной план . Вычисляем значение функции цели:

.

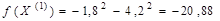Оцениваем положение исследуемой точки:

,

следовательно, точка 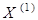находится вне ОДР. При переходе к очередной точке необходимо использовать штрафную функцию (так как очевидно из рис.21, что решение будет находиться только в области положительных значений переменных, то в рекуррентной формуле не будем применять принцип выбора максимума):

2 и т е р а ц и я ,

.

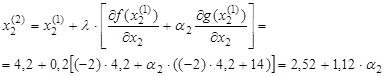Получили два уравнения, где неизвестными являются коэффициенты α_i. Наиболее простой метод их расчета возможен исходя из положения, что возвращаемая в ОДР точка не должна далеко отклоняться от границы ОДР. Из рис.21 видно, что решение задачи находится в области, где обе координаты точки D могут быть близки значению 4. Теперь, если принять, что , то, ориентируясь на точные решения приведенных уравнений, можно принять . Тогда получаем очередной план: . Вычисляем значение функции:

.

Оценим план на принадлежность к ОДР:

.

Следовательно, исследуемая точка вернулась в ОДР.

3 и т е р а ц и я ,

.

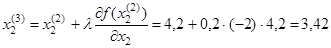Вычисляем значение функционала: ,

Определяем принадлежность плана к ОДР:

.

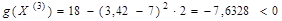План находится вне ОДР, поэтому следующая точка ищется с учетом штрафной функции.

4 и т е р а ц и я

Очевидно, что , так как структура и содержание рекуррентной формулы одинакова для обеих переменных (см. объяснение ниже).

Получили необычный результат. Мы повторно получили предыдущий план. Если не изменить шаг итерации и коэффициент α, то произойдет зацикливание решения. Очевидно также, что мы находимся достаточно близко от оптимального плана. Поэтому примем шаг на пятой итерации . Учтем также, что точка находится в ОДР.

5 и т е р а ц и я

Значение второй координаты будет тем же, т.е. .

Вычисляем значение функции цели: .

Проверяем план на принадлежность к ОДР:

.

Следовательно, план находится в ОДР и так как достаточно близко к оптимальному, еще уменьшим шаг вычислений, приняв .

6 и т е р а ц и я

и соответственно .

Вычисляем значение функционала:

Проверяем план на принадлежность к ОДР:

.

План принадлежит к ОДР.

7 и т е р а ц и я

.

Соответственно .

Вычисляем значение функционала:

Проверяем план на принадлежность к ОДР:

.

Точка вышла из ОДР. Тем не менее, оценивая величины и , лежащие по разную сторону границы ОДР, можно утверждать об их достаточно высокой близости. Оценим ее в виде абсолютной точности:

%.

Получено решение с точностью до 1%.: , . Точное решение задачи: , . В завершение поясним некоторые моменты, связанные с геометрической трактовкой рассмотренной задачи.

В задаче поверхностью отклика функции цели являлся параболоид вращения, у которого ось симметрии совпадала с вертикальной осью координатной системы. Для такой поверхности любая вертикальная плоскость, проведенная через ось, даст на поверхности параболоида кривую (например, кривая ОDFC, рис.21)– наикратчайшее расстояние между любой точкой, лежащей на кривой, и вершиной (глобальным экстремумом) поверхности параболоида. Симметричность поверхности функции цели относительно вертикальной оси координат подтверждается структурной однотипностью формул частных производных функции цели, т.е. градиента функции.

На рис.21 представлены положения четырех первых точек процесса итерации. На первом итерационном шаге совершен переход от точки к точке . Он выполнен по поверхности параболоида и в проекции на горизонтальную плоскость направление перехода осуществлено по прямой, направленной из точки к центру координатной системы, где находится глобальный максимум вогнутого параболоида. Это полностью согласуется с математической трактовкой метода наискорейшего спуска, согласно которому перемещение исследуемой точки должно идти в направлении максимального значения градиента функции цели. Очевидно, так должна перемещаться любая исследуемая точка согласно рекуррентной формуле метода наискорейшего спуска.

Так как план 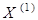вышел из ОДР, то подключение штрафной функции заставило исследуемую точку вернуться в ОДР. В результате на втором шаге итерации точка попала в положение точно на линию, соединяющую центр ОДР и точку Е с центром координатной системы (т.е. в плоскость сечения А-А, рис.21). На ней же расположена и точка оптимального решения – точка D. Это случайность, но так как координаты центра Е одинаковы, то линия ОЕ – биссектриса прямого угла первого квадранта. Следовательно, любая точка, лежащая на ней, будет иметь равные координаты, т.е , а линия ОЕ - это одновременно и траектория с максимальным градиентом. Поэтому все дальнейшие исследуемые точки обязательно должны были лежать только на этой линии, что в принципе мы и наблюдали в ходе аналитических вычислений.

Поиск по сайту: