Математическая модель транспортной задачи в сетевой постановке

На сети с n вершинами и m дугами расположено множество поставщиков и потребителей , известны ресурсы каждого поставщика и потребности каждого потребителя 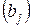. Задана стоимость перевозки груза по каждой дуге и ее пропускная способность .

Требуется найти оптимальную схему прикрепления потребителей к поставщикам таким образом, чтобы минимизировать тонно-пробег груза или суммарные затраты на перевозки.

В этом случае экономико-математическая модель задачи имеет вид

,

при условии что ;

;

;

,

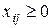где – грузопоток по дуге ;

– стоимость перевозки груза по дуге или ее длина;

– пропускная способность дуги .

Пример

Рассмотрим алгоритм решения транспортной задачи на сети без ограничения по пропускной способности.

На рис.1 представлена симметричная транспортная сеть с 11 вершинами (станциями отправления и назначения) и 17 звеньями (участками, соединяющими пункты отправления и назначения). В каждом звене проставлено число, характеризующее расстояние (длину звена ) между соседними вершинами, соединенными данным звеном.

В круглых скобках против каждой вершины отмечены резервы ресурсов со знаком (+) и потребностей со знаком (–). Необходимо минимизировать суммарное расстояние перевозок продукции.

Рис. 1. Исходная транспортная сеть

Решение

1. Проверяем условие баланса . Составляем первоначальный план, при котором все ресурсы поставщиков должны быть отправлены и весь спрос потребителей удовлетворен. Стрелками показываем направление грузопотоков, а цифрами над ними – количество перевозимой продукции (рис. 2).

Из пункта отправления 1 идут две дуги (1,2) и (1,9) до пунктов потребления. Груз можно развозить произвольно. Например, в пункт 9 отправить грузопоток 50, а в пункт 2 – оставшиеся 250. Оставив 80 ед. груза в пункте 2, оставшиеся 170 повезти в пункт 3 и т.д. Из пункта 10 груз можно перевозить в пункты 11 и 7, 40 и 60 единиц соответственно. Из пункта отправления 6 груз в количестве 200 единиц можно везти в пункт 5, затем оставшиеся 140 ед. – в пункт 4.

Вариантов составления первого опорного плана множество. Рассмотрим один из них. Из пункта отправления 1 направим грузопоток по дуге (1,2) 250 ед. груза и по (1,9) – 50 ед. В пункте 2 оставляем 80 единиц груза и оставшиеся 170 единиц направим по дуге (2,3). Из пункта отправления 10 направим по дуге (10,3) 60 ед., а по дуге (10,11) – 40 ед. груза. Суммарный грузопоток в пункт 3 по дугам (2,3) и (10,3) составит 230 ед. груза. Оставив в пункте 3 120 единиц груза оставшиеся 110 направляем по дуге (3,4).

Из пункта отправления 6 груз отправляем по дугам (6,7) – 100 ед. и (6,5) – 100 ед. Оставив 60 ед. груза в пункте 6, оставшиеся 40 единиц направим по дуге (5,4). К пункту потребления идут два грузопотока (3,4) – 110 ед. и (5,4) – 40 ед., что составляет в сумме потребность в 150 единиц груза.

Рис. 2. Первоначальный план распределения

2. Присваиваем потенциалы вершинам. Например, вершине 1 присваиваем любой достаточно большой потенциал, чтобы впоследствии не иметь дело с отрицательными числами (допустим, 100). Потенциалы остальных вершин вычислим по правилу: при продвижении по дугам в направлении следования грузопотока к потенциалу предыдущей вершины прибавляем длину звена, а при движении по дугам против потока эту длину из потенциала предыдущей вершины вычитаем.

Это правило легко объясняется тем, что движение по потоку происходит от станции отправления груза до станции его назначения, поэтому общее расстояние перевозок будет расти. В обратном направлении – от станции назначения до станции отправления, следовательно, общее расстояние перевозок уменьшается. Число грузопотоков в невырожденном плане равно , n – число вершин транспортной сети. Схема перевозок с проставленными потенциалами показана на рис. 3.

Рис. 3. Первоначальный план с потенциалами вершин

3. Для дуг без грузопотоков проверяем условие оптимальности . В противном случае план перевозок не является оптимальным, т.к. при переводе грузопотоков на данные дуги общее расстояние перевозок уменьшится. В примере отсутствуют грузопотоки на дугах (8,9), (1,10), (3,11), (5,11), (6,10), (7,10) и (9,10).

На дуге (1,10) ;

(3,11) ;

(5,11) ;

(6,10) ;

(7,10) ;

(8,9) .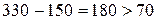

Условие оптимальности нарушено на дугах (8,9) и (7,10).

4. Выбираем дугу (8,9) с наибольшим нарушением условия оптимальности и направляем по ней грузопоток от меньшего потенциала к большему по замкнутому контуру, состоящему из дуг с грузопотоками и выбранной дуги без грузопотока с нарушением условия оптимальности. Этот контур единственный и состоит из дуг (8,9)-(8,7)-(7,6)-(6,5)-(5,4)-(4,3)-(3,2)-(2,1)-(1,9).

Продвигаясь по контуру в направлении от меньшего потенциала дуги с нарушением условия оптимальности к большему (в данном случае против часовой стрелки), находим дугу (8,6) с наименьшим встречным грузопотоком, равным 75. Вычитая его из всех встречных и прибавляя ко всем попутным грузопотокам, получаем улучшенный план перевозок (рис. 4).

Рис. 4. Улучшенный план перевозок

Повторяем шаги 2 и 3. Теперь нет необходимости заново вычислять все потенциалы вершин сети. Достаточно исправить потенциалы тех вершин, где изменилось направление грузопотоков. В нашем случае это вершина 8. На рис. 4 видно, что при новом варианте распределения грузопотоков последние отсутствуют на дугах (7,8), (1,10), (3,11), (5,11), (6,10), (7,10), (9,10). Проверяем эти дуги на оптимальность.

На дуге (7,8)

(1,10) ;

(3,11) ;

(5,11) ;

(6,10) ;

(7,10) ;

(9,10) .

Условие оптимальности нарушено на дуге (7,10). Повторяем шаг 4. Находим замкнутый контур, состоящий из дуг с потоками и дуги (7,10). Это контур, образованный из дуг (7,10), (10,3), (3,4), (4,5), (5,6), (6,7). Движение по нему следует осуществить от вершины с меньшим потенциалом до вершины с большим потенциалом (от 10-й к 7-й). В данном случае против часовой стрелки. В этом контуре с наименьшим встречным потоком является дуга (6,7) с грузопотоком мощностью 25 ед. Это число прибавляем ко всем попутным и вычитаем из всех встречных потоков. В результате получаем новый вариант перевозок (рис. 5):

Рис. 5. Оптимальный план

Снова повторяем шаги 2 и 3. Теперь потенциал меняется лишь к вершине 7 и равен 210.

В новом варианте без грузопотоков остались дуги (6,7), (7,8), (1,10), (3,11), (5,11), (6,10) и (9,10). Проверяем на оптимальность дуги (6,7) и (7,8) в связи с тем, что изменился только потенциал вершины 7

(6,7) ;

(7,8) .

Получим оптимальный план.

На рис. 6 изображена лишь та часть сети, по которой проходят грузопотоки:

Рис. 6. Дерево грузопотоков

Эта часть сети не содержит замкнутых контуров. Сеть такого вида называется деревом. Доказано, что оптимальный план перевозок однородного груза на сети без ограничений по пропускной способности всегда образует дерево с числом звеньев n – 1, то есть число звеньев с грузопотоками должно быть на единицу меньше числа вершин. Поэтому первоначальный базисный план не должен содержать замкнутых контуров. В некоторых случаях дуги с грузопотоками могут образовывать два и более дерева, не соединенные друг с другом. Это так называемый случай вырождения. Для решения такой задачи необходимо оба или больше дерева соединить дугой с нулевым грузопотоком, но так, чтобы не замкнуть контур, и эту дугу включить в базис для определения потенциалов вершин.

Вопросы для самопроверки

1. В чем смысл транспортной задачи в сетевой постановке?

2. Как составляется первоначальный опорный план в транспортной задаче на сети?

3. Сколько дуг с грузопотоками содержит невырожденный план задачи?

4. Каково условие оптимальности решения задачи?

5. Как находятся потенциалы вершин сети?

6. Как строится контур и определяется направление грузопотока в контуре?

7. Как определяется величина перемещаемого по контуру грузопотока?

8. Проведите аналогию решения методом потенциалов транспортной задачи в матричной форме и сетевой постановке.

Задачи для самостоятельного решения

Найти оптимальное решение транспортной задачи на сети

1.

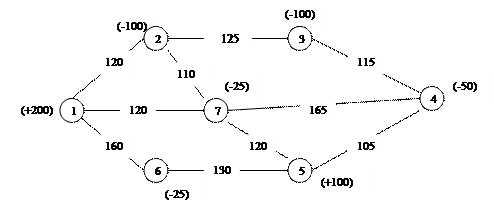
2.

3.

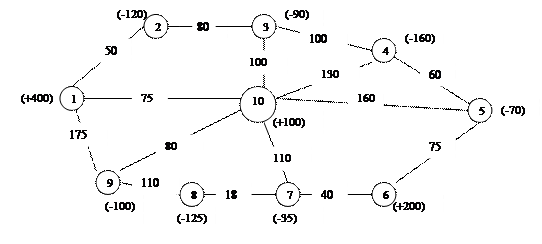
4.

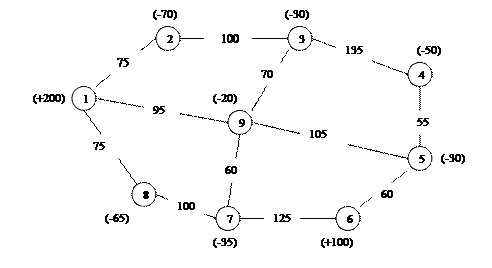
5.

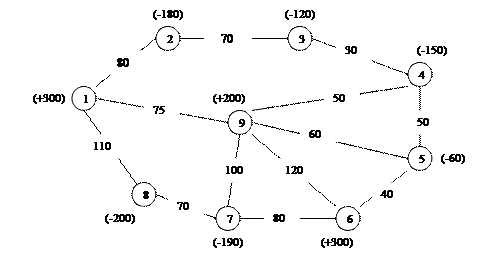
6.

7.

8.

9.

10.

Поиск по сайту: