Классическое правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств. Необходимые условия второго порядка в задаче оптимизации типа равенств

(1) (2)

Опр. Задача (1),(2) наз нормальной в точке , если среди обобщенных векторов множ-лей Л., соотв. в точке нет таких для кот. , то вектор в таком случае наз. норм-ным.

Опр. Точка наз. обыкновенным планом для задачи (1)-(2), если -ЛНЗ (3). Усл. (3) наз. условием Люстерика.

Т-ма1 Оптим. план для з.(1),(2) явл нормальнам тогда и только тогда, когда он обыкновенный.

Д-во:Пусть -оптим. норм. план. Это значит, что сущ. вектора Среди которых Предположим, что при этом не явл. обыкновенным, это означает – ЛЗ. Тогда соотнош.(4) возможно при усл. 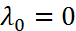, что -нормальный план.

Пусть план явл. обыкнов., тогда вектора -ЛНЗ. План явл. оптимальным, то согласно обобщ-му правилу множ-лей Лагранжа сущ. множитель (,) ,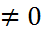что вып. рав-во . Предпол., что план не явл. не явл. нормальным. Но в силу того, что среди множ-лей Л. есть не нулевые из (5) следует что градиенты огран-ий ЛЗ, что противоречит обыкновенности плана .

Т-ма2(классич. правило мн. Л.) Пусть оптим. План з-чи (1),(2) и пусть при , 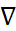ограничений -ЛНЗ. Тогда сущ. ед-ный в-р множ-лей Л. (), такой, что справедливы рав-ва 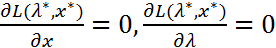(6).

Док-во. В усл. т-мы 2 план явл обыкн., след-но по т-ме 1 норм., тогда 1 из усл.(6) есть усл. из обобщ-го правила множлей Л. при условии, ., 2 из (6) совпадает с системой ограничений.

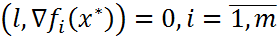Т-ма3.(необх. Усл. 2-го порядка) Пусть ф-я зад. (1)-(2) дважды непрерывно диф., еслит. явл. т. лок. мин-ма этой з-чи и явл. обыкн-й т. с-мы огран-й и есть соотв. В-р множ-лей Л., тогда квадр-я форма, составленная по вторым произ. ф-ции Л. по переменным задачи выполненным в т. не отриц. опред. Для всех в-ров удовл. условиям (7), т.е. для всех в-ров удовл.(7) выполн.(8) .

Поиск по сайту: