Многомерная задача безусловной оптимизации

Многие методы решения многомерной задачи нелинейного программирования основаны на сведении этой задачи к задаче безусловной оптимизации. Поэтому рассмотрим 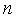-мерную задачу оптимизации без ограничений

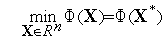
(1)

По аналогии с одномерной задачей, для того, чтобы точка 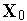являлась минимумом функци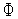и () необходимо выполнение условия стационарности функции 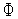() в точке 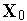или, что то же самое, необходимо, чтобы точка 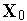была стационарной точкой функции ():

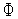(2)

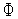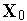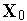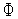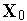Положим, что функции () дважды непрерывно дифференцируема в окрестности точки . Для поиска достаточного условия достижения этой функцией в точке минимума, разложим () в окрестности точки в ряд Тейлора:

(3)

Здесь 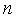-мерный вектор-столбец достаточно малых величин , – -матрица Гессе.

По аналогии с одномерной задачей, для того, что в точке 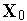достигался минимум функции 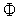(), необходимо, чтобы разность была положительной. Поскольку , то из (3) следует, что для выполнения этого условия необходимо, чтобы матрица Гессе () была положительно определена в точке .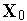

Таким образом, справедлива

Теорема 1. Если функция 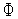() дважды непрерывно дифференцируема в окрестности точки Rⁿ, то необходимыми и достаточными условиями минимума этой функция в точке 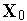являются условия:

(4)

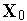() - положительно определена

Таким образом, теорема 1 определяет необходимые и достаточные условия минимума в многомерная задача безусловной оптимизации.

Заметим, что условие 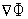(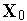)=0 является только необходимым условием минимума в многомерной задаче безусловной оптимизации.

По аналогии с одномерной задачей точками, в которых функция 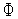() достигает своего наименьшего значения, могут быть либо ее стационарные точки функции, либо критические точки функции (точки недифференцируемости).

Поэтому так же, как в одномерной задаче, точку, в которой функция 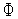() принимает наименьшее значение нужно искать, сравнивая значения этой функции во всех стационарных и критических точках.

Поиск по сайту: