Задача выпуклого программирования

Рассмотрим 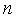-мерную задачу выпуклого программирования

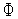() – выпуклая функция, – выпуклое не пустое ограниченное и замкнутое множество допустимых значений вектора варьируемых переменных. Напомним, что по определению выпуклая функция является непрерывной.

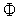Во внутренних точках множества допустимых значений функция () достигает минимального значения в точках, которые являются ее либостационарными точками функции

Важные свойства задачи выпуклого программирования определяют две следующие теоремы.

Теорема 1. Если внутренняя точка 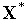множества является точкой локального минимума в задаче выпуклого программирования, то в этой точке функция достигает глобального минимума.

Доказательство. Положим, что в точке 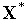функция не достигает наименьшего во множестве значения. Тогда существует точка , для которой . Рассмотрим сечение . Функция () достигает в точке =0 наибольшее значение. Действительно, поскольку

Это значит, что существует окрестность точки 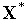и некоторое такие, что

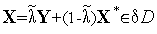. Но тогда , что противоречит условию теоремы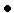

Из теоремы следует, что во всех точках локального минимума выпуклая функция имеете одинаковые значения.

Поиск по сайту: