Пример 1. Рассмотрим не строго выпуклую квадратичную функцию , определенную в области = (см

Рассмотрим не строго выпуклую квадратичную функцию , определенную в области 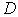= (см. рис. 1). Все локальные минимумы этой функции равны нулю и расположены на прямой - 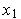+ =0.

MATLAB-программа:

x=-2:0.06:2;

y=x;

[X,Y]=meshgrid(x);

Z=(X+Y).^2;

V=[0.025,0.5,1,2,4,8];

[C,h]=contour(X,Y,Z,V);

clabel(C,h);

Рис. 1. К прим. 1

Теорема 2. Функция 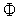(), строго выпуклая функция на выпуклом множестве, имеет в этом множестве не более одной точки минимума (глобального)

Условие существования решения задачи выпуклого программирования дает следующая теорема.

Теорема 3. Пусть функция 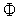() выпукла на выпуклом множестве и дифференцируема в точке 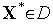Тогда для того чтобы эта точка была точкой минимума функции 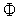(), необходимо и достаточно, чтобы для любой точки выполнялось неравенство

(1)

Необходимость. Рассмотрим сечение функции 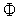(). Функция () определена на отрезке [0,1], имеет в точке =0 локальный минимум и дифференцируема в этой точке. Следовательно (равенство нулю имеет место в том случае, когда точка 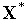является внутренней точкой множества ). По правилу дифференцирования сложной функции

Достаточность. Пусть в точке 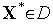выполнено неравенство (1). Рассмотрим сечение функции 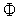(), где – произвольная точка из множества . Поскольку 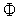() выпукла во множестве , то функция () также выпукла на отрезке [0,1]. Кроме того, из неравенства (1) следует, что (0) 0. Это означает, что () - неубывающая отрезке [0,1] функция, т.е. (0) (1). Последнее неравенство означает, что и в точке 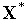функция 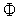() принимает наименьшее в области значение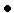

Теорему 3 иллюстрирует рис. 2, линии уровня на котором получены с помощью следующей MATLAB-программы:

x=-2:0.06:-0.1;

y=x;

[X,Y]=meshgrid(x);

Z=100.*(Y-X.^2).^2+(1-X).^2;

V=[2,8,32,125,250,500,1000,2000];

contour(X,Y,Z,V);

[C,h]=contour(X,Y,Z,V);

clabel(C,h);

Точка на рис.рис. 2 является точкой локального минимума, поскольку не существует такой точки , что скалярное произведение ( (),( - )) отрицательно. Точка , например, не является точкой локального минимума, так как существуют такие точки , что скалярное произведение ( (),( - )) отрицательно.

Рис. 2. К теореме 3.

Заметим, что если точка 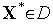является внутренней точкой множества , то условие (1) эквивалентно условию . Таким образом, условие (1) можно рассматривать как обобщение необходимого условия минимума в многомерной задаче безусловной оптимизации.

Поиск по сайту: