АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема Куна-Таккера для задачи нелинейного программирования с ограничениями типа неравенств

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.1. Двойственная задача линейного программирования
  6. I. 4.1. Первая теорема двойственности
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  9. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  10. I. Ситуационные задачи и тестовые задания.
  11. I. Цель и задачи дисциплины
  12. I.5.3. Подготовка данных для задачи линейного программирования

Рассмотрим задачу нелинейного программирования

(1)

 

где () – произвольная функция,

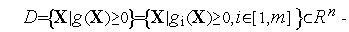
не пустое, ограниченное замкнутое множество.

Нам понадобятся далее понятия множителей Лагранжа и функции Лагранжа для задачи нелинейного программирования с ограничениями типа неравенств. Функция Лагранжа для задачи (1) с ограничениями (2) определяется формулой

 

(2)

 

где - -вектор множителей Лагранжа.

Нам понадобятся также понятия активных и неактивных ограничений. В точке локального минимума задачи (1), (2) каждое из ограничений выполняется либо в виде равенства , либо в виде неравенства . Ограничения первого вида называются активными ограничениями. Остальные ограничения называются неактивными ограничениями.

Кроме того, нам понадобится также понятие условия регулярности для задачи нелинейного программирования с ограничениями типа неравенств. Если точка 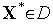и ограничения активны, то условие линейной независимости векторов называется условием регулярности ограничивающих функций в точке 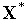. Это условие означает, что, например, при 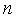=2 количество ограничивающих функций, проходящих через точку 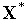, не должно превышать 2 и в точке 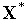векторы (), () не должны быть коллениарны Например, на рис. 1 в ситуации (а) количество ограничивающих функций, проходящих через точку 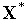, превышает размерность вектора варьируемых параметров, в ситуации (б) в точке 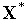градиенты (), 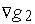() ограничивающих функций коллениарны.

Рис. 1. Ситуации, в которых не выполняется условие регулярности двумерной задачи.

Исключительно большое значение в теории и практике решения задач нелинейного программирования имеет следующая теорема (теорема Куна-Таккера для задачи условной оптимизации с ограничениями типа неравенств).

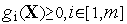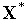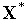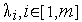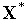Теорема 1 (Куна-Таккера). Пусть функция и функции имеют непрерывные частные производные в некоторой окрестности точки и пусть эта точка является точкой локального минимума функции при ограничениях , удовлетворяющих в точке условию регулярности ограничивающих функций. Тогда существуют такие неотрицательные множители Лагранжа , что для функции Лагранжа точка является стационарной точкой функции, т.е.

(3)

 

Заметим, что в отличие от правила множителей Лагранжа, теорема 1 требует знакоопределенности множителей Лагранжа 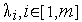. Отметим также, что теорема не запрещает того, чтобы все множители Лагранжа 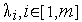были равны нулю.

Поясним смысл теоремы на примере.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)