Метод покоординатного спуска (метод релаксации)

Стро­го го­во­ря, по­ко­ор­ди­нат­ный спуск не от­но­сит­ся к ме­то­дам пря­мо­го по­ис­ка, по­сколь­ку на­пра­в­ле­ние дви­же­ния здесь оп­ре­де­ля­ет­ся не свой­ст­ва­ми ми­ни­ми­зи­ру­е­мой функ­ции, а ори­ен­та­ци­ей ко­ор­ди­нат­ных осей. Од­на­ко мы вклю­чи­ли его в этот раз­дел как ме­тод, не тре­бу­ю­щий вы­чис­ле­ния про­из­вод­ных.

Ме­тод по­ко­ор­ди­нат­но­го спу­с­ка (на­зы­ва­е­мый так­же ме­то­дом ре­ла­к­са­ции) яв­ля­ет­ся са­мым про­стым сре­ди ме­то­дов ми­ни­ми­за­ции функ­ций не­сколь­ких пе­ре­мен­ных. Пусть за­да­но началь­ное при­бли­же­ние x₀. Фи­к­си­ру­ем все ко­ор­ди­на­ты кро­ме x₁, и най­дем наи­мень­шее значение F(x), дви­га­ясь от x₀ па­рал­лель­но оси Ox₁. До­с­тиг­нув наи­низ­шей точки в дан­ном на­пра­в­ле­нии (обоз­начим ее x₁), фи­к­си­ру­ем все ко­ор­ди­на­ты, кро­ме x₂, и бу­дем ис­кать наи­мень­шее значение функ­ции, дви­га­ясь па­рал­лель­но оси Ox₂. По­с­ле то­го, как мы за­кончили по­иск вдоль ка­ж­дой из N ко­ор­ди­нат­ных осей и до­с­тиг­ли точки x_N, про­дол­жим спуск, сно­ва дви­га­ясь поочеред­но вдоль осей Ox₁, Ox₂ и т. д. Этот про­цесс про­дол­жа­ет­ся до тех пор, по­ка даль­ней­шее по­ни­же­ние значения функ­ции не пре­кра­тит­ся ли­бо пе­ре­ме­ще­ния те­ку­щей точки не ста­нут мень­ше за­дан­но­го преде­ла.

Рис. 5. Поиск минимума методом покоординатного спуска

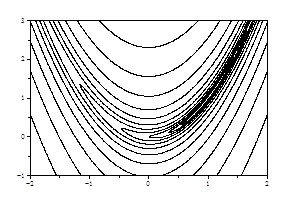Рис. 6. Функция Розенброка

Та­ким об­ра­зом, тра­е­к­то­рия спу­с­ка от точки x₀ к ми­ни­му­му пред­ста­в­ля­ет со­бой ло­ма­ную ли­нию, со­сто­я­щую из вза­им­но ор­то­го­наль­ных от­ре­з­ков, как по­ка­за­но на рис. 5. Глав­ный не­до­с­та­ток за­ключает­ся в том, что при этом ни­как не учиты­ва­ет­ся ре­аль­ная фор­ма по­верх­но­сти. Ес­ли функ­ция по­хо­жа на изо­б­ра­жен­ную на рис. 5, т. е. ли­нии уров­ня бли­з­ки к ок­ру­ж­но­стям или эл­лип­сам и не слиш­ком силь­но вы­тя­ну­ты, то ме­тод ре­ла­к­са­ции ра­бо­та­ет впол­не удо­в­ле­тво­ри­тель­но. Од­на­ко в бо­лее сло­ж­ных си­ту­а­ци­ях, вро­де по­ка­зан­ной на рис. 6 функ­ции Ро­зен­бро­ка , ме­тод ста­но­вит­ся не­эф­фе­к­тив­ным. Эта функ­ция яв­ля­ет­ся стан­дарт­ным те­с­том для ис­пы­та­ния ме­то­дов ми­ни­ми­за­ции. Опи­сы­ва­е­мая ею по­верх­ность пред­ста­в­ля­ет со­бой уз­кий па­ра­бо­личес­ки изо­г­ну­тый «ов­раг» с кру­ты­ми скло­на­ми, причем дно ов­ра­га по­ло­го спу­с­ка­ет­ся к точке ми­ни­му­ма с ко­ор­ди­на­та­ми [1, 1]. На рис. 6 ось z име­ет ло­га­риф­мичес­кий мас­штаб, так как ди­а­па­зон из­ме­не­ния функ­ции в изо­б­ра­жен­ной об­ла­с­ти слиш­ком ве­лик. В раз­ных точках дна ов­ра­га функ­ция при­ни­ма­ет значения от 0 до 5.5, то­г­да как ма­к­си­маль­ная вы­со­та скло­нов пре­вы­ша­ет 2500. Не­тру­д­но ви­деть, что на­чав­ши, на­при­мер, по­ко­ор­ди­нат­ный спуск от точки [-1, 1], при­дет­ся сде­лать боль­шое чис­ло ко­рот­ких ша­гов, по­сколь­ку на­пра­в­ле­ние, ве­ду­щее к ми­ни­му­му, по­сто­ян­но ме­ня­ет­ся.

Поиск по сайту: