Основные общие своиства злп

1. Каждому опорному/базисному решению ЗЛП соответствует крайняя угловая точка выпуклого многогранника D, представляющего собой область допустимых решений задачи (*),и наоборот.

2. Целевая функция z ЗЛП (*) достигает своего оптимума в крайней точке выпуклого многогранника D, порожденного условиями задачи (*). Если целевая функция z ЗЛП (*) достигает своего оптимума более чем в одной крайней точке выпуклого многогранника D, порожденного условиями задачи (*), то она достигает своего оптимума в любой точке, являющейся выпуклой комбинацией данных крайних точек.

Рассмотрим следующую основную задачу линейного программирования:

Z=C₁X₁+C₂X₂+…+C_NX_N à max

при ограничениях

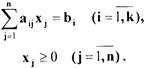
Перепишем ограничения этой задачи в векторной форме:

x₁P₁+x₂P₂+…+x_nP_n=P₀ (1.3

где Р₁,..., Р_n и Р₀ - k-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членов системы ограничений основной задачи:

Определение 1.3. План х=(x₁,x₂,...,X_n) называется опорным планом основной задачи линейного программирования, если его положительные коэффициенты (х_j>0) стоят при линейно независимых векторах Рj.

Так как векторы Рj являются k-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше числа k.

Определение 1.4. Опорный план называется невырожденным, если он содержит ровно k положительных компонент, в противном случае он называется вырожденным.

Свойства задач линейного программирования тесным образом связаны со свойствами выпуклых множеств.

Определение 1.5. Пусть х⁽¹⁾,...х^(m)- произвольные точки евклидова пространства Rⁿ. Выпуклой линейной комбинацией этих точек называется сумма: a₁х⁽¹⁾+...+ а_mх^(m), где а_i (альфа) - произвольные неотрицательные числа, сумма которых равна 1.

Определение 1.6. Множество называется выпуклым, если вместе с любыми двумя своими точками оно содержит и отрезок прямой, соединяющий эти точки.

Определение 1.7. Точка X выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации каких-нибудь двух других различных точек данного множества.

Сформулируем первое свойство задач ЛП.

Теорема 1.1. Множество планов любой задачи линейного программирования является выпуклым (если оно не пусто).

Определение 1.8. Непустое множество планов задачи линейного программирования называется многогранником решений, а всякая угловая точка многогранника решений - вершиной.

Сформулируем второе свойство задач ЛП.

Теорема 1.2. Если задача линейного программирования имеет оптимальный план, то экстремальное значение целевая функция задачи принимает в одной из вершин многогранника решений. Если экстремальное значение целевая функция принимает более чем в одной вершине, то она принимает его на ребре (грани), содержащем эти вершины.

Теорема 10.3. Если система векторов в разложении (10.14) линейно независима и такова, что

где все , то точка является угловой точкой многогранника решений.

Теорема 1.4. Если =( ₁, ₂,..., n)- вершина многогранника решений, то векторы Рj, соответствующие положительным _j >= 0, линейно независимы.

Поиск по сайту: