 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод дихотомии. Пусть дана функция f(x), унимодальная на отрезке [a;b]
Пусть дана функция f(x), унимодальная на отрезке [a;b]. Обозначим a0 = a и
b0 = b. Поиск минимума начинают с выбора на отрезке неопределенности [a0;b0 ] двух симметричных относительно середины точек:
 где d - параметр метода.
где d - параметр метода.
Сравнивая вычисленные в точках a1 и b1 значения функций f(a1) и f(b1), в силу унимодальности функции можно провести сокращение отрезка неопределенности следующим образом:
1) если f(a1) £f(b1), то x*Î[a0;b1] (Рис. 1.6.1-3.а);
2) если f(a1) >f(b1), то x*Î[a1;b0] (Рис. 1.6.1-3.b).

а) b)
Рис. 1.6.1-3
Если описанную процедуру принять за одну итерацию, то алгоритм поиска минимума можно описать следующим образом. Опишем k+1 итерацию, исходя из того, что k -й отрезок неопределенности найден [ak;bk]:
1. Вычисляются
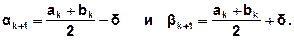
2. Находят значения f(ak+1) и f(bk+1).
3. Находят k+1 -й отрезок неопределенности по правилу:
если f(ak+1) >f(bk+1), то x* Î[ak+1;bk],
если f(ak+1) £f(bk+1), то x*Î[ak;bk+1]).
Вычисления проводятся до тех пор, пока не выполнится неравенство

где Dn – длина n -го отрезка неопределенности.
Заметим, что от итерации к итерации Dn убывает и при n®¥ стремится к величине 2d, оставаясь больше этой величины. Поэтому добиться при некотором значении n длины отрезка неопределенности  | меньше
| меньше  заданной точности можно лишь выбирая 0<d<e/2.
заданной точности можно лишь выбирая 0<d<e/2.
Длину конечного интервала неопределенности, обеспечивающего заданную величину e, можно вычислить по формуле

Положив Dn= e, можно определить соответствующее количество итераций:

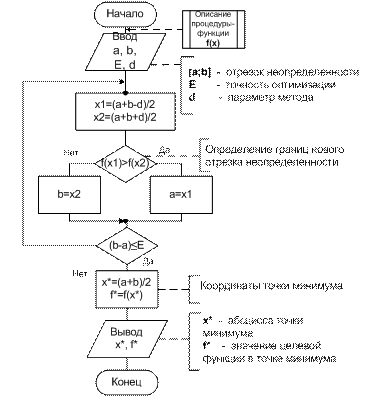
Схема алгоритма метода дихотомии приведена на рис. 1.6.1-4.
|
Рис.1.6.1-4. Схема алгоритма поиска минимума методом дихотомии
Пример 1.6.2-1. Найти минимум функции f(x)=x3-x+e-х на отрезке [0;1]c точностью e и вычислить количество итераций, требуемое для обеспечения точности.
Выберем d =0.001 и положим a = 0;b = 1; 

| n | a | b | a1 | b1 | f(a1) | f(b1) | Dn |
| 0.499 | 0.501 | 0.23239 | 0.23067 | 0.501 | |||
| 0.499 | 0.7485 | 0.7505 | 0.14392 | 0.14435 | 0.2515 | ||
| 0.499 | 0.7505 | 0.62375 | 0.6257 | 0.15486 | 0.15413 | 0.12675 | |
| 0.62375 | 0.7505 | 0.68613 | 0.6881 | 0.14040 | 0.14023 | 0.06437 | |
| … | ….. | ….. | ….. | …. | ….. | ….. | …. |
| 0.701719 | 0.71931 | 0.70951 | 0.7115 | 0.13954 | 0.13959 | 0.00979 |
Приe = 0.1 x*=0.7183 f(x*)=0.1399, а при e = 0.01 x*=0.7066 f(x*)=0.13951 
.
Поиск по сайту: