АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ

Читайте также:
  1. F полезности и ее оптимизация
  2. Анализ и оптимизация СГ
  3. Анализ и оптимизация стоимости проекта.
  4. Безусловная оптимизация для одномерной унимодальной целевой функции
  5. Вопрос 6. Оптимизация полезности
  6. Вопрос 68. Управление денежными активами и ликвидностью: анализ, оптимизация, формы регулирования и контроль состояния.
  7. Вопрос 69. Управление запасами: анализ, цели формирования, оптимизация и контроль
  8. Вопрос 8. Управление денежными активами и ликвидностью: анализ, оптимизация, формы регулирования и контроль состояния.
  9. Вопрос 9. Управление запасами: анализ, цели формирования, оптимизация и контроль
  10. Выпуклая оптимизация. Условие выпуклости. Субградиентный метод выпуклой оптимизации. Метод растяжения пространства. Метод эллипсоидов.
  11. ГЛАВА 1. ОПТИМИЗАЦИЯ ЧИСЛЕННОСТИ КАДРОВ
  12. Дальнейшая оптимизация решения

4.1. Задача многокритериальной оптимизации. Многокритериальная предпочтительность решений

В задачах математического программирования, рассмотренных ранее, необходимо среди допустимых решений выбрать оптимальное по одному заранее выбранному критерию. Между тем, в реальных экономических задачах приходится искать наилучшее решение, руко­водствуясь несколькими различными целями. Причем довольно часто эти цели в той или иной степени противоречат друг другу.

Примерами противоречивых целей в задачах реальной экономики являются минимальные затраты и минимальное время выполнения ра­бот, максимальная доходность финансовой операции и ее минимальный риск или, например, максимальная прибыль, максимальная эффектив­ность вложенных средств и максимальный объем производства.

Математически такая задача содержит область допустимых реше­ний, которая может иметь любую природу, и несколько целевых функций, значение которых должно максимизироваться или миними­зироваться в данной области. Максимизация и минимизация целевых функций легко сводятся друг к другу умножением на -1, поэтому, не нарушая общности, можно считать, что данная задача имеет вид:

fi(х) → mах (i = 1, 2,…, n),

x D,

х -?,

где D — область допустимых решений.

Отметим, что в этой задаче х может быть векторным параметром.

Если количество целевых функций fi в задаче (4.1.1) больше од­ной, то данная задача является задачей многокритериальной оптими­зации.

В экономических задачах допустимая область обычно задается системой уравнений и неравенств, к которой могут быть добавлены некоторые дополнительные ограничения, например ограничения на целочисленность переменных.

Пример 4.1. Парикмахерская может производить два вида про­дукции: мужские и женские прически, причем мастера, работающие в парикмахерской, являются универсалами. Женская прическа отнимает два часа работы мастера и приносит 10 у.е. прибыли. Мужская при­ческа отнимает один час работы мастера и приносит 4 у.е. прибыли. Общий ресурс работы мастеров составляет 40 ч. Социальный заказ, установленный для парикмахерской при ее открытии, состоит в мак­симальном количестве обслуженных клиентов.

Если через х1 и х2 обозначить количество мужских и женских причесок, сделанных в парикмахерской за рассматриваемый проме­жуток времени, то математическая модель рассматриваемой задачи будет иметь вид:

z1 =4x1 + 10х2 → max,

z2 = х1 + х2 → max,

х1 + 2x2 ≤ 40

х1, х2 Z,

х1, х2 ≥ 0,

х1, х2 -?

В данной задаче оптимальность производственного плана парик­махерской определяется по двум критериям: критерию максимальной прибыли и критерию максимального количества обслуженных клиен­тов. Этим критериям соответствуют целевые функции z, и z2.

В задаче многокритериальной оптимизации (4.1.1), рассматривае­мой в прямой постановке, как правило, нет решений, поскольку цели, выражаемые различными критериями, часто являются противополож­ными. Поэтому оптимальные значения целевых функций достигаются при разных допустимых решениях. Например, в примере 4.1 целевая функция z1 достигает своего максимума при х1 = 0, х2 = 20, а функ­ция z2 — при х1 = 40, х2 = 0.

Несмотря на отсутствие оптимального решения в задаче (4.1.1), на практике приходится делать выбор в пользу какого-либо одного до­пустимого варианта. Поэтому в многокритериальных задачах необхо­димо сравнивать различные допустимые решения, хотя далеко не все из них будут сравнимы.

Смысл сравнения различных допустимых решений в многокрите­риальной задаче состоит в следующем. Для каждого допустимого ре­шения задачи определяется оценка, которая зависит от значений целе­вых функций f1, f2,… fп. В совокупности все эти функции состав­ляют векторный критерий f = (f1, f2,… fп).

Оценкой допустимого решения x D задачи (4.1.1) называется вектор f(x) = (f1(x), f2(х), … fn(x)) Rn.

Теперь, какова бы ни была природа множества D, можно сравни­вать не его элементы, а их векторные оценки. То есть предпочтитель­ность на множестве D можно заменить предпочтительностью оценок на множестве Rn.

Если отношение предпочтительности на множестве D обозначить символом 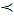, то для любых х, у D х 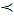у означает, что f(х) < f(у) на множестве Rn.

Сложность состоит в том, что и на множестве Rn элементы срав­нимы далеко не всегда. Часто встречается ситуация, когда среди двух допустимых решений одно лучше по одному критерию, а второе - по другому. Например, в задаче (4.1.2) векторная оценка решения (0; 20) имеет вид (200; 20), а векторная оценка решения (40; 0) — (160; 40). По этим оценкам видно, что рассматриваемые решения несравнимы.

Для выбора лучшего решения на множестве несравнимых реше­ний необходимы специальные процедуры, которые вкладывают в по­нятие лучшего решения некоторый конкретный смысл. Такие проце­дуры будут рассмотрены в § 4.4.

Сейчас же будет рассмотрено, какой смысл можно вложить в поня­тие предпочтительности на множестве оценок допустимых решений.

 

 

4.2. Эффективные решения многокритериальных задач. Различные виды эффективности

Основная сложность анализа многокритериальных задач состоит в том, что в них проявляется эффект несравнимости решений. В даль­нейшем допустимые решения многокритериальных задач будем также называть исходами. На практике задача сравнения различных исходов обычно ставится следующим образом: среди всех допустимых реше­ний выбрать одно наилучшее. При этом при наличии нескольких кри­териев разные люди вкладывают в понятие «наилучшее решение» различный смысл. Если одно из двух рассматриваемых возможных решений лучше по одному из используемых критериев, а второе — по другому критерию, то в различных ситуациях лучшими могут быть признаны разные решения. Такие решения называются несравнимы­ми. Выбор лучшего из них зависит не только от конкретных условий задачи, но и от предпочтений лица, принимающего решения (ЛПР).

Однако иногда можно сравнивать по качеству некоторые исходы, удовлетворяющие наложенным ограничениям независимо от пред­почтений ЛПР. Например, если одно из двух возможных решений лучше другого по всем рассматриваемым критериям, то ему, конечно, следует отдать предпочтение.

Математически отношения между объектами, когда некоторые из них можно сравнивать, а некоторые несравнимы, называются отно­шениями частичного порядка или отношениями строго частичного порядка. При этом отношение имеет некоторые естественные свойст­ва. В задаче многокритериальной оптимизации (4.1.1) на множестве D допустимых решений можно ввести отношение строго частичного порядка.

Итак, пусть х, у — два допустимых решения задачи (4.1.1), т.е. х D y D. Будем говорить, что х строго предпочтительнее у, если решение х лучше решения у по всем критериям. Такое отноше­ние строгого предпочтения на множестве D будем записывать сле­дующим образом: х у строго.

Если считать, что все целевые функции задачи (4.1.1) максимизи­руются, то: х у строго, если для всякого i = 1, 2,…п fi(x) > fi(y).

Отношение строгого предпочтения можно ослабить: будем гово­рить, что допустимое решение х доминирует допустимое решение у, если х не хуже у по всем критериям и строго лучше хотя бы по од­ному из них. Такое отношение будем обозначать следующим образом: х у. В случае максимизируемых целевых функций х у означает, что выполнены два условия:

1) для всякого i = 1,2,..., п справедливо неравенство fi(x) ≥ fi(y)

2) существует j, такое, что fj (х) > fj (у).

Отношение доминирования, введенное на множестве допустимых решений D, называется также доминированием по Парето. Оно от­ражает совершенно естественный взгляд на сравнение различных ис­ходов по нескольким критериям, как, впрочем, и отношение строгого предпочтения, введенное до этого.

Таким образом, на множестве D допустимых решений задачи (4.1.1) введены два различных отношения: 1) строгого предпочте­ния и 2) доминирования по Парето. С практической точки зрения каж­дое из них имеет свои преимущества и недостатки. Отношение стро­гого предпочтения является бесспорным, однако слишком много объ­ектов оказываются несравнимыми. Поэтому отношение доминирова­ния по Парето получило большее распространение в экономических исследованиях.

Поясним суть двух рассматриваемых отношений на примере зада­чи (4.1.2). Рассмотрим два допустимых решения этой задачи: х = (5; 10) и у = (10; 5). Значения целевых функций для этих решений соответственно равны:

z1(x) = l20, z2(x) = 15;

z1(y) = 90, z2(x) = 15.

Решения x и у равнозначны по второму критерию, но х пред­почтительнее по первому критерию. Поэтому нельзя сказать, какое решение является строго предпочтительным. Если использовать от­ношение строгой предпочтительности, то исходы х и у несравнимы.

Однако исход х доминирует исход у по Парето.

Как уже говорилось, на практике обычно требуется выбрать луч­шее решение, причем существенная (если не самая главная) часть за­дачи — определить смысл, вкладываемый в данное понятие. Однако часто задачу можно значительно упростить, если уменьшить количе­ство рассматриваемых исходов.

Действительно, если имеются два допустимых решения х и у, причем х предпочтительнее у, то решение у не может быть лучшим среди всех допустимых решений, потому что х лучше него. Поэтому при выборе наилучшего решения множество допустимых решений можно уменьшить, отбросив те из них, для которых найдется более предпочтительный по какому-либо введенному отношению строгого порядка исход. В результате в рассмотрении останется такая совокуп­ность исходов, в которой любые два исхода несравнимы. Подобное представление об уменьшении рассматриваемого множества решений лежит в основе понятия эффективного решения. И поскольку на мно­жестве допустимых решений введено два различных отношения стро­гого частичного порядка, то можно ввести два различных понятия эффективного решения.

Рассмотрим задачу (4.1.1). Допустимое решение х 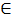D называется эффективным, если не существует у, такого, что у х, т.е. для любого у 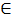D не выполняется хотя бы одно из двух условий:

1) для всякого i = 1, 2,… п fi(y) ≥ fi(x);

2) существует j, такое, что fj(у) > fj(х).

Эффективное решение задачи (4.1.1) называется также решением, оптимальным по Парето, или Парето-оптимальным решением.

Допустимое решение х D называется слабо эффективным (или оптимальным по Слейтеру), если не существует y D, такого, что у х строго, т.е. для всякого у D существует число i, такое, что

fi(y) ≤ fi(x)

В заключение рассмотрим понятие оптимальности по Парето и по Слейтеру на примере следующей задачи многокритериальной опти­мизации:

z1 = 4х1 + 10х2 → max,

z2 = х1 + х2 → max,

z3 = х2 → max,

х1 + 2х2 ≤ 40,

х2 < 15,

х1, х2 ≥ 0,

х1, х2 -?

 

Множество допустимых решений этой задачи изображено на рис. 4.1.

Множество допустимых решений представляет собой много­угольник ОАВС. Для всех точек этого многоугольника, кроме точек ломаной ABC, можно найти решения, которые являются более пред­почтительными как в отношении строгого предпочтения, так и в от­ношении доминирования по Парето. Для этого необходимо рассмот­реть точки, лежащие выше, тогда увеличатся значения всех трех целе­вых функций. Так как для всех точек многоугольника ОАВС, кроме точек ломаной ABC, существуют допустимые точки, лежащие выше их, то эти точки не являются оптимальными ни по Парето, ни по Слейтеру.

Все точки отрезка АВ безразличны по отношению к критерию z3, поэтому они несравнимы в отношении сильного предпочтения. При этом при движении вдоль отрезка АВ от точки А к точке В растут значения критериев z1 и z2. Но при движении по отрезку ВС от точ­ки В к точке С значение функции z2 растет, а значение функции z1 уменьшается. Поэтому точки отрезка ВС несравнимы в отношении доминирования по Парето, а все точки интервала АВ доминируются по Парето точкой В.

Таким образом, в задаче (4.2.1) оптимальными по Парето являют­ся точки отрезка ВС, а оптимальными по Слейтеру — точки ломаной ABC.

Понятие эффективного решения является фундаментальным в ре­шении задач многокритериальной оптимизации, поскольку позволяет значительно уменьшить число рассматриваемых решений.

4.3. Построение Парето-эффективной границы

Парето-оптимальность некоторого исхода означает, что он не мо­жет быть улучшен ни по одному из критериев без ухудшения по ка­кому-либо другому критерию.

Пусть совокупность функций F = {f1..., fm} осуществляет ото­бражение множества допустимых решений D на множестве Y Rm. Подмножество Y называется эффективной границей (множест­вом точек, оптимальных по Парето), если для любого вектора у не существует вектора X, который доминирует вектор F-1(у).

Для наглядного представления доминирования по Парето и Парето-оптимальности рассмотрим случай двух позитивных критериев f1 и f2. Критерий fj называется позитивным, если лицо, принимающее решение, стремится к его увеличению, и негативным, если ЛПР стре­мится к его уменьшению.

Векторные оценки исходов представим точками координатной плоскости Of1f2 (рис. 4.2).

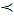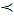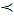На рис. 4.2 изображено множество допустимых исходов для дис­кретного случая. Здесь Парето-оптимальными являются исходы (4, 5, 7, 8). При этом каждый исход, не являющийся Парето-оптимальным, доминируется по Парето некоторым Парето-оптимальным исходом, не обязательно одним (например, 6 5, 6 7, 10 7, 10 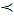5 (по Парето) и т.д.).

В случае когда множество допустимых исходов является непрерывным, их векторные оценки «заполняют» некоторую область Q на плоскости (рис. 4.3).

В этом случае множество Парето-оптимальных исходов (полужирная линия γ на рис. 4.3) представляет собой часть границы Q, точнее, ее «северо-восточную» часть, так как целью ЛПР при позитивных критериях f1, f2 является увеличение их значений, что соответствует движению внутри области Q вправо и вверх.

Замечания. 1. Область, изображенная на рис. 4.3, является выпуклой, т.е. вместе с любыми двумя своими точками она содержит весь соединяющий их отрезок. В случае невыпуклой области ее Парето-оптимальная граница может иметь более «экзотический» вид (на­пример, состоять из отдельных линий и (или) точек).

Пример такой Парето-оптимальной границы представлен на рис. 4.4.

2. Предположим, что в задаче принятия решения имеются крите­рии разного характера. Пусть, например, f1 — негативный, а f2 — по­зитивный критерий. Тогда целью ЛПР будет уменьшение критерия f1 и увеличение критерия f2, что соответствует движению на координат­ной плоскости «влево и вверх». В этом случае Парето-оптимальная граница области Q представляет собой ее «северо-западную» часть (рис. 4.5).

Для позитивных критериев f1, f2 некоторую ломаную ABC (рис. 4.6) можно принять за множество, оптимальное по Парето, если для любой точки К этой ломаной построенный в ней «уголок» пересе­кается с множеством точек ломаной только в точке К.

4.4. Процедуры решения многокритериальных задач

Рассмотренные примеры показывают, что в типичных случаях Па-рето-оптимальных (эффективных) исходов может быть несколько, а в непрерывном случае — бесконечное множество. Невозможно дать однозначный ответ на вопрос, какой из эффективных исходов следует считать оптимальным для общего случая. Нужно иметь в виду, что любые два эффективных исхода несравнимы относительно доминиро­вания по Парето.

В самом деле, если для двух исходов (a, ) D выполняется усло­вие > а (по Парето), то исход а не может быть Парето-оптимальным. Если нет информации об относительной важности кри­териев f1 и f2, то рациональный выбор между а1 и а2 сделать невоз­можно. (Отметим, что нельзя сделать рациональный выбор и в такой ситуации, когда, например, имеется 10 критериев, причем а1 лучше а2 по одному критерию, но хуже по девяти остальным. Понятно, что в некоторых реальных случаях превосходство по одному критерию мо­жет «перевесить» превосходство по всем остальным.)

Методика исследования задач принятия решений для многокрите­риального случая может быть связана с различными подходами.

Первый вариант. Для заданной многокритериальной зада­чи нахождения решения (ЗНР) находится множество ее эффективных решений, а выбор конкретного решения из множества Парето-оптимальных решений предоставляется ЛПР.

Второй вариант. Производится сужение множества Парето-оптимальных исходов (в идеале — до одного элемента) с помощью некоторых формализованных процедур, что облегчает окончательный выбор исхода для ЛПР. Это сужение может быть произведено при наличии дополнительной информации о критериях или свойствах эф­фективного решения.

Рассмотрим данный подход подробней. Будем считать, что много­критериальная ЗНР задана в виде

(D; f1,…,fm),

где f1 - позитивные критерии, j = 1, т.

При указании нижних границ критериев дополнительная инфор­мация имеет вид:

fj (a*) ≥ γj,

где γj - нижняя граница по j-му критерию;

а* — оптимальный исход, а* D.

Очевидно, что при увеличении значений уj, j = 1,m, Парето-оптимальное множество «сокращается». Пример, представленный на рис. 4.7, демонстрирует это обстоятельство для случая двухкритериальной задачи с критериями f1 и f2.

На рис 4.7 точками отмечены концы М, N Парето-оптимальной границы области Q. Участок АВ, например, соответствует двум требованиям: f1 (а*) > у"1, f 2 (а*) > у"2. Основной недостаток данного метода заключается в том, что эффективное решение здесь субъективно, так как зависит от величины нижних границ критериев, а также предпоч­тений ЛПР.

 

Субоптимизация

При субоптимизации выделяют один из критериев, а по всем ос­тальным назначают нижние границы. Оптимальным при этом считается исход, максимизирующий выделенный критерий на множестве исхо­дов, оценки которых: по остальным критериям не ниже назначенных.

Пусть, например, f1 — выделенный критерий, а γj — нижняя гра­ница для j-гo критерия, где j = 2, т. Тогда оптимальным считается тот исход а* 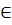D, на котором достигается максимум функции f1, рас­сматриваемой на множестве D1 = { а 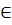D: f1(a) > γj (j = 2,т)}.

Возьмем, например, для ЗНР, представленной на рис. 4.6, в качестве выделенного критерия f1, а в качестве нижней границы по критерию f2 — величину γ'2. Тогда оптимальное решение соответствует точке пересе­чения горизонтальной прямой, проведенной через γ'2, с Парето-оптимальной границей. Очевидно, что при увеличении нижней границы критерия f2 максимум функции f1 уменьшается (не увеличивается).

С помощью метода субоптимизации задача многокритериальной оптимизации превращается в задачу «обычной» оптимизации на су­женном допустимом множестве. Окончательное решение здесь также имеет субъективный характер.

 

Лексикографическая оптимизация

Лексикографическая оптимизация основана на упорядочении кри­териев по их относительной важности. Далее процедура развивается по шагам. На первом шаге отбираются исходы, которые имеют мак­симальную оценку по важнейшему критерию.

Если такой исход единственный, то его и считают оптимальным. Если же таких исходов несколько, то среди них отбирают те, которые имеют максимальную оценку по критерию, следующему за важней­шим, и т.д. К недостаткам данного метода следует отнести следующее:

1) трудности в установлении упорядоченности критериев по их относительной важности;

2) фактически принимается во внимание только первый важней­ший критерий (например, следующий за ним по важности критерий учитывается только тогда, когда первый достигает максимума на не­скольких исходах);

3) в результате лексикографической процедуры не всегда опреде­ляется единственный исход.

 

Метод обобщенного критерия

Весьма важен метод обобщенного критерия — процедура, которая «синтезирует» набор оценок по заданным критериям, называемых ча­стными или локальными, в единую численную оценку, выражающую итоговую полезность для ЛПР данного набора оценок. Таким образом, задание обобщенного критерия сводит задачу многокритериальной оптимизации к задаче однокритериальной оптимизации с целевой функцией f.

Наиболее распространенным обобщенным критерием является взвешенная сумма частных критериев, которая превращает вектор­ную оценку у = (у1,…уm) в скалярную оценку

φ(y) = a1y1 +... + аmуm, аj ≥ 0, j = 1, т

(иногда требуют, чтобы = 1).

Числа аj - называют весовыми коэффициентами. Весовой коэффи­циент аj интерпретируется как «показатель относительной важности» j-го критерия, т.е. чем больше аj, тем больший «вклад» вносит оценка по j-му критерию в итоговую оценку φ(у).

Теорема 4.1. Пусть Q Y- произвольное множество векторных оценок. Если векторная оценка у =(у1 ,… уm ) доставляет максимум функции φ(y) = ; где все > 0, то векторная оценка у является Парето-оптимальной на множестве Q.

Доказательство. Предположим противное, т.е. то, что существует векторная оценка у' = (у'1,… у'т) Q, которая доминиру­ет по Парето векторную оценку у*. Тогда при всех j = 1, т выполня­ется неравенство у'j ≥ уj , причем хотя бы для одного индекса j нера­венство выполняется как строгое. Умножая эти неравенства на аj, суммируя их по j = 1,т и учитывая, что все аj > 0, получаем:

т.е. φ(y) > φ(y.), что противоречит условию теоремы.

Замечание. Обратное утверждение справедливо не всегда. Например, в случае выпуклости множества Q можно доказать лишь, что векторная оценка у., Парето-оптимальная на множестве Q, доставляет максимум функции φ(y) = , с некоторым вектором неотрицательных весов aj > 0.

Метод перехода от нескольких критериев f1… fm к одному, за­даваемому новой функцией φ = , называется также сверткой.

Если в качестве выступают объемы выпуска продукции разного вида и

ЛПР стремится к увеличению каждого показателя 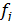, то в качестве aj могут выступать просто цены продуктов, а свертка будет означать переход от натуральных к одному стоимостному показателю.

Нередко выбор весов (аj) является достаточно сложной задачей, для решения которой используют экспертные оценки, а также методы параметрического программирования.

Следует отметить, что критерии fj могут быть разнородными, поэтому обычно свертке предшествует нормировка. Один из ее вари­антов состоит в том, что для каждого критерия 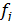находится макси­мальное значение 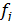+ из области допустимых значений и минималь­ное значение 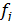- на множестве Парето-оптимальных решений. После этого каждая функция 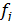заменяется на 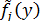по следующему правилу:

Если все являются линейными функциями, то после преобра­зования и нормировки все будут также линейными функциями.

Если веса нормированы, т.е. = 1, аj > 0, j = 1, т, то свертка φ = принимает значения на отрезке [0,1].

Метод параметрического программирования

Пример 4.2. Рассмотрим пример оценки весов (аj) с помощью метода параметрического программирования:

Z1 (х) = -4х1 + 6х2 → max,

Z2(x) = 2х1 + x2 → max,

-х1 + х2 ≤ 3,

х2 ≤ 5,

х1 + х2 ≤ 10,

х1 ≤ 8,

х1 ≥ 0, х2 ≥ 0.

Решение. Пусть используется свертка без нормировки:

Z = a1Z1 + a2Z2 → max.

Если для весов выполняется нормировка =1, то можно записать:

Z = a1Z1 +(l – a1)Z2 = (2 - 6a1)x1 +(l + 3a1)x2 → max.

Результаты исследования зависимости решения (х1, х2) от выбора веса аj с помощью метода параметрического программирования представлены в табл. 4.1.

Таблица 4.1

а1 х1(а1) х2(а1)
0< а1 < 1/11    
а1 = 1/11 8λ + 5(1 - λ) 2λ + 5(1 - λ)
1/11 < а1 < 1/3    
а1 = 1/3 5λ + 2(1 - λ)  
1/3 < а1 < 1    

 

 

Из табл. 4.1 видно, что достаточно лишь грубо оценить, в какой
области лежит а1: а1 (0, 1/11) или а1 (1/11;1/3), или а1 (1/3;1), поскольку точное значение а1 внутри какой-либо из указанных об­ластей не оказывает влияния на значения х1, х2.

Метод «идеальной точки»

Пример 4.3. Рассмотрим задачу производственного планирова­ния и метод «идеальной точки».

Для выпуска двух видов продукции Р1 и Р2 используются три вида ресурсов (R1, R2, R3), которые можно приобрести в количестве не бо­лее 20, 15 и 39 единиц соответственно.

Задана матрица А, элементы которой показывают нормы расхода ресурсов на выпуск единицы продукции каждого вида:

12

А= 11

Известны также цены продуктов: С1 = 17 руб., С2 = 12 руб. за еди­ницу продукции соответствующего вида; цены ресурсов: q1 = 1 руб., q2 = 1 руб., q3 = 4 руб. за единицу ресурса соответствующего вида.

При оценке различных вариантов плана используются три показа­теля:

Z1 — общий объем выпускаемой продукции (в денежном выражении);

Z2 — общий объем прибыли;

Z3 — отношение прибыли к затратам на приобретение ресурсов.

Для формализации задачи введем переменные х1 и х2, которые оз­начают планируемые объемы выпуска продукции Р1 и Р2. Соответст­венно имеем:

х1+ 2х2 ≤ 20,

х1 + х2 ≤ 15,

3х1 + х2 ≤ 39,

х1 ≥ 0, х2 ≥ 0.

Область, определяемая этими ограничениями, представляет собой выпуклый многоугольник с вершинами в точках О (0, 0), А(0, 10), B(10,5), С(12,3), D(13,0).

Введем три целевые функции:

Z1 = 17х1 + 12х2 → max,

Z2 = 3х1 + 5x2 → max,

Z3 = (3х1 + 5x2) / (14x1+7x2) → max.

В табл. 4.2 приведены значения целевых функций в вершинах об­ласти допустимых решений.

Таблица 4.2

Вершина     Показатель А(0, 10) В(10, 5) С(12, 3) D(13, 0)
Z1        
Z2        
Z3 50/70 55/175 51/189 89/182

 

 

Из табл. 4.2 видно, что если ориентироваться на общий объем про­дукции (критерий Z1), то оптимальным будет решение x1 = 12, х2 = 3 (точка С). Если в качестве основного критерия использовать показа­тель прибыли (критерий Z2), то оптимальным решением будет x1 = 10, х2 = 5 (точка В). По критерию Z3 наилучшим является решение x1 = 0, х2 = 10 (точка А).

Выбор конкретного плана (точки х = (х1, х2)) на границе (А, В, С) области допустимых значений зависит от значимости показателей Z1, Z2, Z3 для ЛПР.

Метод «идеальной точки» состоит в том, что ЛПР указывает об­щий принцип — найти такое решение х, при котором значения fJ(х) как можно меньше отклоняются от оптимальных соответствующих показателей fj*. При выборе конкретного варианта реализации дан­ного принципа следует соблюдать осторожность. Допустим, что в ус­ловиях предыдущего примера ЛПР учитывает только критерии Z1 и Z2. Из табл. 4.2 следует, что Z*1 = 228, Z*2 = 55. Для любого допусти­мого плана X расстояние от (Z2(x), Z2(x)) до «идеальной точки» (Z*1, Z*2) = (228, 55) можно оценивать несколькими способами, кото­рые с точки зрения ЛПР могут оказаться далеко не эквивалентными.

Способ 1.

р (| Z1 (х), Z2 (х) |, Z1*, Z2* |) = | Z1 (х) –Z1*| + |Z2 (х) - Z2*|.

Имеем

Z,(x)<Z*, Z2(x)<Z2,

следовательно, возможно следующее преобразование:

р(| Z, (х), Z2 (х) |, | Z*, Z2* |) = 228 + 55 — Z, (х) - Z2 (х) =

= 283 – Z1(х) – Z2(х) → min.

Очевидно, что это эквивалентно

L(Z) = Z1(х) + Z2(х) → max.

Таким образом, при оценке отклонений от «идеальной точки» с помощью обычных модулей многокритериальная задача сводится к однокритериальной задаче на максимум обычной суммы частных критериев, что может не соответствовать представлениям ЛПР.

Способ 2.

р (| Z1(х), Z2 (х) |, | Z*1 Z2* |) = → min.

При таком выборе расстояния многокритериальная задача с линей­ными целевыми функциями сводится к однокритериальной задаче с квадратичной целевой функцией и линейными ограничениями, которая может быть решена одним из методов квадратичного программирования.

Метод последовательных уступок

Метод последовательных уступок решения многокритериальных задач применяется в том случае, когда частные критерии упорядочены в порядке убывания важности.

Предположим, что все критерии позитивны и упорядочены. Нахо­дим максимальное значение Z*1 первого по важности критерия в об­ласти допустимых решений, решив задачу:

Z1() → max; х Q.

Затем исходя из практических соображений и принятой точности назначается величина допустимого отклонения δ1 > 0 критерия Z1 и находится максимальное значение второго критерия Z2 при условии, что значение первого должно отклоняться от максимального не более чем на величину допустимой уступки, т.е. решается задача вида

Z2 () → max,

Z1 () ≥ Z*1 – δ1.

Снова назначается величина уступки δ2 > 0 по второму критерию, которая вместе с первой используется при нахождении условного экс­тремума третьего частного критерия, и т.д. Наконец, выявляется экс­тремальное значение последнего по важности критерия Zm при условии, что значение каждого из первых т - 1 частных критериев отличается от экстремального не более чем на величину допустимой уступки. Полу­ченное на последнем этапе решение считается оптимальным. Заметим, что этот метод не всегда приводит к эффективному решению.

Пример 4.4. Решить задачу методом последовательных уступок:

Z1 = -х1 + 2х2 → max,

Z2 = 2х1 + х, → max,

Z3 = х1 - 3х2 → max,

х1 + х2 ≤ 6,

1 ≤ х1 ≤ 3,

1 ≤ x2 ≤ 4,

х1 ≥ 0.

Решение. Будем считать, что допустимые уступки по первым двум критериям равны δ1 = 3, δ2 = 5 /3.

Максимизируем функцию Z1 что легко сделать графически (рис. 4.8).

Получаем х*1 = 1, х2* = 4, Z*1 = Z1max = Z1(A) = 7. Переходим к мак­симизации Z2 при условиях х1 + х2 ≤ 6; 1 ≤ х1 ≤ 3; 1 ≤ х2 ≤ 4 и допол­нительном ограничении, позволяющем учесть, что по критерию Z нельзя уступить более чем на 3. Так как Z1* - δ1 = 4, то дополнитель­ное ограничение имеет вид:

-х1 + 2х2 ≥ 4.

Решаем задачу:

Z2 = 2х1 + х2 → max,

х1 +х2 ≤ 6,

1 ≤ х1 ≤ 3,

1≤ х2 ≤ 4,

-х1 + 2х2 ≥ 4.

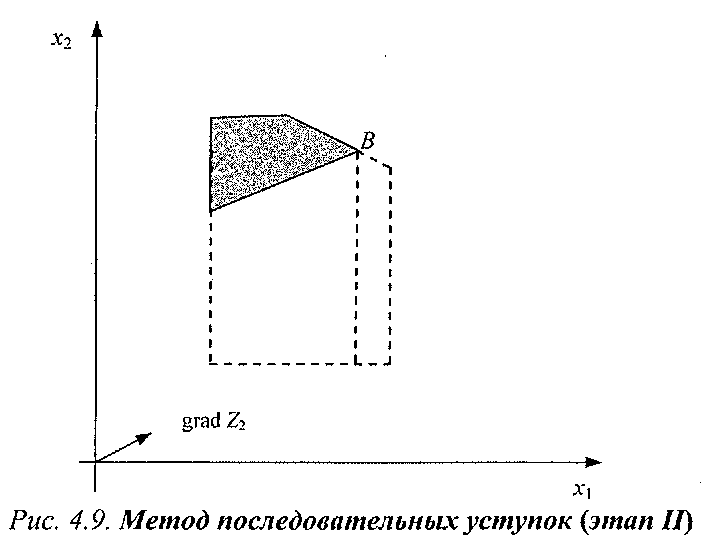
Решая графически эту задачу, получаем оптимальную точку 5(8/3, 10/3), Z2max = Z2* =Z2(B) = 26/3 (рис. 4.9).

Теперь уступаем по критерию Z2 на δ2, получаем второе дополни­тельное ограничение 2х1 + х2 ≥ 7.

Максимизируем Z3, решая следующую задачу:

Z3 = х1 - 3х2 → max,

х1 + х2 ≤ 6,

1≤ х1 ≤ 3,

1 ≤ х2 ≤ 4,

-х1 + 2х2 ≥ 4,

2х1 + х2 ≥ 7.

Из рис. 4.10 представлено графическое решение данной задачи.

 

 

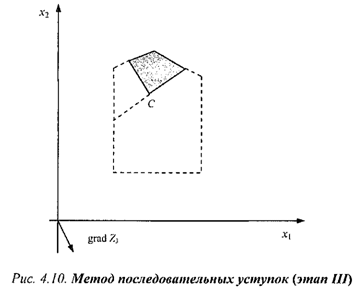
Координаты точки С: х1 = 2, х2 = 3. Эти значения и есть решение трехкритериальной задачи, полученное методом последовательных уступок.

Вопросы и задачи

Чем отличается задача многокритериальной оптимизации от об­щей задачи математического программирования?

Что является оценкой допустимого решения в задаче многокрите­риальной оптимизации?

Объясните смысл понятия доминирования по Парето.

Какие решения задачи многокритериальной оптимизации назы­ваются оптимальными по Парето?

Инвестор рассматривает четыре инвестиционные операции со слу­чайными эффективностями, которые описываются случайными ве­личинами Е1, Е2, Е3, Е4 с известными рядами распределения:

(0, 1/2) (2, 1/4) (4, 1/8) (16, 1/8);

(2,1/2) (4,1/4) (6,1/8) (18,1/8);

(0, 1/4) (4, 1/4) (6, 1/3) (12, 1/6);

(2, 1/4) (6, 1/4) (8, 1/3) (14, 1/6).

Определите, какие из этих операций оптимальны по Парето.

Объясните, почему независимо от предпочтений лица, прини­мающего решение, лучшим может быть признано только реше­ние, оптимальное по Парето.

Чем отличается оптимальность решений по Парето и по Слейтеру?

Найдите эффективные и слабоэффективные решения для задачи (4.2).

Что представляет собой множество Парето-оптимальных исходов, если множество допустимых исходов является непрерывным?

Как выглядит Парето-оптимальная граница для двух негативных критериев, если допустимая область имеет вид, изображенный на рис. 4.5?

Решите задачу (4.3) для свертки всех критериев с равными весо­выми коэффициентами.

В чем смысл нормировки критериев, проводимой перед их сверткой?

Решите задачу (4.2) методом идеальной точки, если в качестве расстояния взять обычное расстояние R2.

Решите задачу (4.2) методом последовательных уступок, считая, что критерии упорядочены в порядке убывания важности, причем величина уступки по первому критерию равна 20.

Постройте область компромисса в задаче двухкритериальной оп­тимизации:

Z1 = (2х1 + 3х2) → max,

Z2 = (х1 - 2х2) → max,

х1 - 2х2 ≤ 1,

х1 + х2 ≥ 1,

-х1 + х2 ≤ 1,

0 ≤ х1 ≤ 3,

0 ≤ х2 ≤ 2.

Методом последовательных уступок решите задачу трехкритери­альной оптимизации:

a) Z1 = (2х1 + 3х2) → max,

Z2 = (2х1 – х2) → max,

Z3 = х2 → min,

δ1 = 9, δ2 = 3, -2x1 + x2 ≤ 2, 2x1 - x2 ≤ 5, 1 ≤ x1 ≤ 4, 1 ≤ x2 ≤ 6;

б) Z1 = х1 → max, Z2 = (х1 + x2) → max, Z3 = (x1 + 2x2) → max, δ1 =5, δ2 = 1,

x1 + x2 ≤ 6, x2 ≤ 3, x1 ≥ 0, x2 ≥ 0.

Библиографический список

1. Вентцель E.C. Исследование операций. Задачи, принципы, мето­дология. М.: Высшая школа, 2001.

2. Гуткин Л.С. Оптимизация радиоэлектронных устройств по сово­купности показателей качества. М.: Советское радио, 1975.

3. Кипи Р.Л., Райфа X. Принятие решений при многих критериях: предпочтения и замещения. М.: Радио и связь, 1981.

4. Лазарев Ю.Н. Алгоритм решения многокритериальных задач управления // Известия Самарского научного центра РАН. 2001. Т. 3. № 1.

5. Ларичев О.И. Наука и искусство принятия решений. М.: Наука, 1979.

6. Ларичев О.И. Теория и методы принятия решений: Учебник. М.: Логос, 2002.

7. Лотов А.В., Поспелова И.И. Конспект лекций по теории и мето­дам многокритериальной оптимизации. М.: Изд-во ВМиК МГУ, 2006.

8. Макаров И.М., Виноградская Т.М., Рубчинский А.А., Соколов В.Б. Теория выбора и принятия решений: Учебное пособие. М.: Наука, 1982.

9. Машунин Ю.К. Методы и модели векторной оптимизации. М.: Наука, 1986.

10. Многокритериальные задачи принятия решений / Под ред. Д.М. Гвишиани и СВ. Емельянова. М.: Машиностроение, 1978.

11. Подиновский В.В. Введение в теорию важности критериев в мно­гокритериальных задачах принятия решений: Учебное пособие. М.: Физматлит, 2006.

12. Подиновский В.В., Гаврилов В.М. Оптимизация по последователь­но применяемым критериям. М.: Советское радио, 1975.

13. Подиновский В.В. Количественные оценки важности критериев в многокритериальной оптимизации // Научно-техническая инфор­мация. 1999. №5. С. 22-25.

14. Подиновский В.В. Математическая теория выработки решений в сложных ситуациях: Учебник. М.: МО СССР, 1981.

15. Подиновский В.В., Ногин В.Д. Парето-оптимальные решения мно­гокритериальных задач. М.: Наука, 1982.

16. ПолищукЛ.И. Анализ многокритериальных экономико-математи­ческих моделей. Новосибирск: Сибирское отделение АН СССР, 1989.

17. Саати Т. Принятие решений. Метод анализа иерархий. М.: Радио и связь, 1993.

18. Симанков B.C. Автоматизация системных исследований: Моно­графия. Краснодар: Кубанский государственный технологический университет, 2002.

19. Соболь КМ. Выбор оптимальных параметров в задачах со мно­гими критериями. М.: Наука, 1981.

20. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптими­зации. М.: Наука, 1986.

21. Хоменюк В.В. Элементы теории многоцелевой оптимизации. М.: Наука, 1983.

22. Штойер Р. Многокритериальная оптимизация: теория, вычисле­ния и приложения. М.: Радио и связь, 1992.

 


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.062 сек.)