 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Свойства выпуклых (вогнутых) функций
Теорема 1.1. Если функции  ,
,  , вогнуты (выпуклы) на выпуклом множестве
, вогнуты (выпуклы) на выпуклом множестве  то функция
то функция  вогнута (выпукла) на
вогнута (выпукла) на  для всех
для всех  ,
,  .
.
Теорема 1.2. Сумма строго вогнутой и вогнутой функций есть функция строго вогнутая.
Теорема 1.3. Если  вогнута (выпукла) на выпуклом множестве
вогнута (выпукла) на выпуклом множестве  и
и  ,
,  ,
,  ,
,  ,
,  , то
, то

| (2.2) |
Теорема 1.4. Пусть  – выпуклое множество, а функция
– выпуклое множество, а функция  выпукла (вогнута) на
выпукла (вогнута) на  , тогда множество
, тогда множество  выпукло для любого
выпукло для любого  (
( – действительное число).
– действительное число).
Если функция  непрерывна на
непрерывна на  , а множество
, а множество  замкнуто, то множество
замкнуто, то множество  замкнуто.
замкнуто.
Теорема 1.5. Пусть множество  выпукло и
выпукло и  . Тогда выпуклая (вогнутая) функция
. Тогда выпуклая (вогнутая) функция 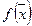 , определенная на
, определенная на  , является непрерывной во всех внутренних точках этого множества.
, является непрерывной во всех внутренних точках этого множества.
Следствие. Если функция 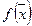 выпукла (вогнута) на всем пространстве
выпукла (вогнута) на всем пространстве  , то функция она непрерывна во всех точках.
, то функция она непрерывна во всех точках.
Определение 3.1. Производной функции 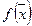 , определенной на множестве
, определенной на множестве  , в точке
, в точке  по направлению
по направлению 
 будем называть число
будем называть число  .
.
Если функция 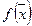 дифференцируема на множестве
дифференцируема на множестве 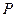 , то
, то 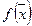 имеет производные по всем направлениям в любой точке
имеет производные по всем направлениям в любой точке  и
и  .
.
Определение 3.2. Направление  в точке
в точке  называется возможным, если существует такое число
называется возможным, если существует такое число  , что для всех
, что для всех  точки
точки  .
.
Очевидно, если  , то любое направление в этой точке является возможным.
, то любое направление в этой точке является возможным.
Теорема 1.6. Пусть множество 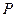 выпукло и
выпукло и  . Тогда вогнутая (выпуклая) функция
. Тогда вогнутая (выпуклая) функция 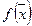 , определенная на множестве
, определенная на множестве 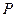 , имеет в каждой внутренней точке этого множества производную по любому направлению
, имеет в каждой внутренней точке этого множества производную по любому направлению  .
.
Теорема 1.7. Пусть функция  выпукла (вогнута) и не убывает в промежутке
выпукла (вогнута) и не убывает в промежутке  (
( не исключается), функция
не исключается), функция  выпукла (вогнута) на выпуклом множестве
выпукла (вогнута) на выпуклом множестве  , причем
, причем  для всех
для всех  . Тогда функция
. Тогда функция  является выпуклой (вогнутой) на множестве
является выпуклой (вогнутой) на множестве 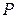 .
.
Следствия из теоремы 1.7.
1) Пусть функция  и выпукла на выпуклом множестве
и выпукла на выпуклом множестве 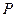 , тогда функция
, тогда функция  при всех
при всех  ,
,  будет выпуклой на
будет выпуклой на 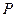 .
.
2) Если функция  выпукла на выпуклом множестве
выпукла на выпуклом множестве 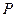 , то выпукла на
, то выпукла на 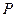 и функция
и функция  ,
,  .
.
3) Если функция  и выпукла на выпуклом множестве
и выпукла на выпуклом множестве 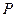 , то выпуклы на
, то выпуклы на 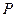 и функции
и функции  ,
,  ,
,  .
.
Поиск по сайту: