 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теоретичні відомості
Вивчення дифракційної гратки
Київ 2010
Лабораторна робота №18
Вивчення дифракційної ґратки
Мета роботи.
Одержати дифракційну картину та визначити період, розділювальну здатність і кутову дисперсію дифракційної гратки.
Теоретичні відомості.
Дифракція світла зумовлена його хвильовою природою і полягає в огинанні світловими хвилями перешкод, тобто у відхиленні їх від прямолінійності поширення. Спостерігається дифракція за умови, що розміри перешкод співрозмірні з довжиною хвилі.
Розрізняють два види дифракції світла.
Дифракція сферичних хвиль, що спостерігається в променях, які після огинання перешкоди сходяться на екрані, розташованому на певній відстані від перешкоди. Така дифракція має назву дифракції за Френелем.
Дифракція плоских світлових хвиль створюється паралельними променями і називається дифракцією за Фраунгофером. В цьому випадку дифракційна картина спостерігається за допомогою збірної лінзи, яка знаходиться між перешкодою і екраном, розташованим у фокальній площині лінзи.
При дифракції виникають так звані максимуми і мінімуми інтенсивності світла, місце розташування яких визначається формою і розмірами перешкоди, на якій дифрагують хвилі.
Посилення і послаблення інтенсивності світла при дифракції пояснюється за допомогою принципу Гюйгенса-Френеля, який полягає в наступному:
· кожна точка фронту хвилі є джерелом вторинних сферичних хвиль;
· вторинні джерела хвиль когерентні, тому збуджені ними вторинні хвилі інтерферують і створюють новий хвильовий фронт.
Згідно з цим принципом прозора для світла частина перешкоди при проходженні крізь неї первинної хвилі може розглядатись як сукупність вторинних джерел. Випромінювані ними вторинні хвилі інтерферують, внаслідок чого відбувається перерозподіл енергії в хвилі, тобто виникнення максимумів і мінімумів освітленості.
При поширенні хвилі в однорідному середовищі з непрозорими перешкодами інтерференція вторинних хвиль призводить до виникнення хвильового фронту, відмінного від хвильового фронту первинної хвилі. Така деформація хвильового фронту еквівалентна зміні напрямку поширення світла і теж призводить до перерозподілу його інтенсивності і виникненню певної дифракційної картини на екрані.
Якщо на вузьку щілину (рис. 1) шириною а спрямувати паралельний пучок променів, то за принципом Гюйгенса-Френеля кожна точка хвильової поверхні АВ буде джерелом коливань, котрі поширюються в усіх напрямках. Результат накладання пучка променів, відхилених під кутом φ від нормалі до площини щілини і зібраних лінзою в одному місці, визначиться різницею ходу АС між крайніми променями цього пучка АД і BE.

Рис. 1. Хід променів при дифракції на щілині.
При різниці ходу, рівній парному числу на півхвиль (цілому числу довжин хвиль λ), увесь пучок можна розкласти на парне число таких сусідніх пучків, різниця ходу між якими буде дорівнювати половині довжини хвилі λ/2. Світлові хвилі, відповідні цим пучкам, будуть мати протилежні фази, тому при накладанні їх на екрані виникнуть мінімуми інтенсивності світла. Зауважимо, що лінза не вносить різниці фаз, бо всі паралельні промені збираються лінзою в одному місці, проходячи від хвильової поверхні до фокуса однакову оптичну довжину ходу. Оскільки
 ,
,
то умова дифракційного мінімуму в цьому випадку запишеться так:

або
 , (1)
, (1)
де k = ±1; ±2; ±3;....
Якщо різниця ходу між крайніми променями пучка складає непарну кількість напівхвиль, то її можна розділити на непарне число променів, для яких різниця ходу для сусідніх променів дорівнює половині довжини хвилі. З поміж них парне число променів за інтенсивністю будуть взаємно знищені, а залишковий промінь забезпечить максимум інтенсивності світла. Тому умова спостереження максимуму інтенсивності при дифракції на одній щілині має вигляд:
 , (2)
, (2)
де k = 0; ±1; ±2; ±3;....
Посередині дифракційної картини (рис. 2) буде спостерігатись світла смуга - дифракційний максимум, який називається центральним, або нульовим, бо в цьому місці будуть сфокусовані лінзою промені, між якими різниця ходу відсутня, тобто вони приходять на екран з однаковими фазами (формула (2) не містить умову нульового максимуму).
На рис. 2 показано хід крайніх променів у пучках, для яких кут φ має різні значення. Ці промені створюють у фокальній площин лінзи максимуми інтенсивності світла. На цьому ж рисунку подано графік розподілу інтенсивності І світла на екрані в залежності від різниці ходу крайніх променів.
 |
Рис. 2.2. Дифракція на щілині.
При освітленні щілини паралельними променями монохроматичного світла по нормалі до щілини на екрані, розташованому у фокальній площині лінзи, будуть спостерігатись світлі (відповідного кольору) паралельні смуги, що чергуються з темними смугами. Освітленість світлих смуг буде зменшуватись при збільшенні їх відстані від центра дифракційної картини. Якщо щілину освітлювати білим світлом, то центральний максимум на екрані теж буде білим, бо в цьому місці промені всіх кольорів будуть відповідно посилювати один одного. По обидва боки від центральної (білої) смуги будуть спостерігатись забарвлені смуги (спектри), які є максимумами інтенсивності для променів, що мають різну довжину хвилі. При цьому промені з більшою довжиною хвилі будуть відхилені в спектрі на більший кут, а з меншою - на менший кут φ, відповідно до формули (2). Ближче до центральної білої смуги буде розміщено максимум фіолетового кольору, а далі від неї - максимуми синього, блакитного, зеленого, жовтого, оранжевого і червоного кольорів, нагадуючи спостерігачеві послідовність кольорів веселки.
Перейдемо до дифракції на гратці.
Система однакових за шириною і паралельних між собою прозорих щілин, розташованих в одній площині і відокремлених одна від одної непрозорими проміжками, називається одномірною дифракційною граткою (ДГ) (рис. 3).
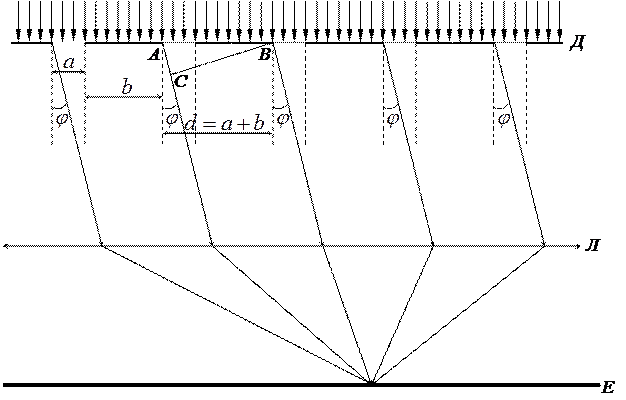
Рис. 3. Хід променів при дифракції на гратці.
Сталою, або періодом гратки називається величина
 ,
,
де а - ширина прозорої щілини, b - відстань між сусідніми щілинами.
Якщо на дифракційну гратку перпендикулярно до її площини падає пучок паралельних променів, то згідно з принципом Гюйгенса-Френеля кожна точка хвильової поверхні АВ кожної щілини буде джерелом вторинних хвиль. Промені всіх пучків, які поширюються під одним і тим же кутом φ відхилення від початкового напрямку променя після проходження ним дифракційної ґратки попадають на лінзу Л. А вона, в свою чергу, буде збирати всі промені в одній точці екрану Е, розташованій у фокальній площині лінзи.
Інтенсивність променів одного пучка, як було з'ясовано при розгляді дифракції від однієї щілини, залежить від кута дифракції φ. Тому для пучків, що вийшли з різних щілин під одним і тим же кутом, інтенсивність буде однаковою. Результат інтерференції таких пучків визначається різницею фаз, з якою промені накладаються на екрані.
При монохроматичному освітленні ґратки ця різниця фаз визначається співвідношенням між різницею ходу і довжиною хвилі. Для крайніх променів в пучках різниця ходу (див. рис. 3)

Якщо величина АС складається з парного числа напівхвиль (ціле число довжин хвиль), то промені накладаються один на одного в однакових фазах і взаємно посилюються. Отже, умова виникнення максимуму освітленості екрана при дифракції на дифракційній гратці має вигляд:
 (3)
(3)
Число m називається порядком головного дифракційного максимуму і може набувати значення:
m = 0; ±1; ±2; ±3;...
Якщо різниця ходу крайніх променів пучків буде дорівнювати непарному числу напівхвиль, то ці промені зустрінуться на екрані в протилежних фазах і послаблять один одного. Таким чином, умова спостереження дифракційного мінімуму освітленості екрана запишеться у вигляді
 , (4)
, (4)
де m = 0; ±1; ±2; ±3;...
Формулами (3) і (4) описано умови спостереження головних дифракційних максимумів та мінімумів для ґраток з будь-якою кількістю щілин, бо пучок світла від кожної нової додаткової щілини поводить себе так само, як і промені від решти щілин ґратки. Положення їх центрів на екрані не залежить від кількості щілин ґратки, а їхня яскравість при збільшені кількості щілин ґратки зростає, бо чим більше щілин, тим більше додається світлових променів
Умовами (3) і (4) не вичерпано всі можливі максимуми і мінімуми інтенсивності світла на екрані після проходження світла крізь дифракційну ґратку. Наприклад, в напрямках, визначених із співвідношення
 ,
,
де m = 0; ±1; +2; ±3;...,
різниця фаз хвиль, що накладаються, складає  . При накладанні хвиль з такою різницею фаз коливання тільки частково посилюються. Цим зумовлена поява додаткових слабко виражених максимумів інтенсивності. Ділянки дифракційної картини, якими відокремлено один від одного ці додаткові максимуми, є додатковими мінімумами.
. При накладанні хвиль з такою різницею фаз коливання тільки частково посилюються. Цим зумовлена поява додаткових слабко виражених максимумів інтенсивності. Ділянки дифракційної картини, якими відокремлено один від одного ці додаткові максимуми, є додатковими мінімумами.
Зауважимо, що при збільшенні кількості щілин у ґратці число додаткових максимумів зростає, проте їх освітленість зменшується, тоді як кількість і розташування головних максимумів залишається незмінною. При достатньо великій кількості щілин ґратки додатковими максимумами нехтують і вважають, що вся енергія хвилі розподіляється тільки між головними дифракційними максимумами інтенсивності світла.
При опроміненні ґратки монохроматичним світлом на екрані чергуються світлі смуги відповідного кольору з темними смугами. При опроміненні ґратки білим світлом дифракційна картина буде складатись із спектрів, розділених темними проміжками. Послідовність чергування кольорів у дифракційних спектрах буде зворотною до розташування кольорових смуг в спектрах, одержаних при дисперсії білого світла. В центрі дифракційної картини буде біла (ахроматична) смуга, бо в цьому напрямі за кутом дифракції φ = 0 при m = 0 виконується умова максимуму інтенсивності світла для хвиль будь-якої довжини.
На практиці важливо відокремити дві спектральні лінії, що мають близькі довжини хвиль, і бачити їх у спектрі як дві лінії, а не одну. Така можливість надається дифракційною ґраткою, вона називається роздільною здатністю ґратки. Якщо довжина хвилі однієї лінії λ, а другої  , то роздільна здатність
, то роздільна здатність
 (5)
(5)
Роздільна здатність є безрозмірною величиною. Вона показує, у скільки разів довжина хвилі спостережуваної лінії має бути більшою від різниці хвиль сусідніх ліній у спектрі, щоб цю лінію можна було бачити як окрему. Внаслідок математичних перетворень виходить, що роздільна здатність ґратки
 , (6)
, (6)
де N - загальна кількість щілин ґратки. З формули (6) видно, що для максимумів одного і того ж порядку роздільна здатність тим більша, чим більша кількість щілин N ґратки задіяна в експерименті, а для однієї й тієї ж ґратки роздільна здатність збільшується при зростанні порядку дифракційного максимуму m.
Ширина дифракційних спектрів характеризується величиною
 ,
,
яка називається кутовою дисперсією ґратки. В цій формулі  - кутова відстань між лініями, які відрізняються довжиною хвилі на
- кутова відстань між лініями, які відрізняються довжиною хвилі на  .
.
Кутова дисперсія чисельно дорівнює кутовій відстані між лініями, що відрізняються за довжиною хвилі на одиницю. Вимірюється кутова дисперсія в рад/м. З теорії дифракційної ґратки випливає, що
 (7)
(7)
Отже, кутова дисперсія для дифракційних максимумів одного і того ж порядку тим більша, чим більша стала ґратки; для однієї й тієї ж ґратки кутова дисперсія збільшується при зростанні порядку максимуму.
Практично дифракційна гратка використовується як основна частина спектральних приладів, призначених для розкладання світлових хвиль в спектр. Останнім часом знайшла практичне використання здатність дифракційної ґратки змінювати напрямок поширення монохроматичного проміння в елементах інтегральної оптики, призначених для передачі інформації на оптичних частотах.
Дифракційні ґратки бувають прозорі та відбивальні.
Прозорі ґратки являють собою скляні або кварцові платівки, на поверхні яких за допомогою спеціальних машин нанесено діамантовим різцем паралельні риски. Щілинами є проміжки між рисками.
Відбивальні ґратки виготовляють шляхом нанесення паралельних рисок на поверхні металевого дзеркала. Виготовлення таких гравірованих ґраток обходиться дорого, тому з них знімають пластикові або желатинові копії (репліки), які майже не поступаються за якістю оригіналові і використовуються як дифракційні ґратки.
Зараз у зв'язку з успіхами в розвитку лазерної техніки з'явилась можливість голографічного виготовлення дифракційних ґраток, на яких на фоточутливій плівці фіксується інтерференційна картина.
У високоякісних ґраток на 1 мм припадає 1200 рисок, а, отже, і стільки ж щілин.
Число п рисок на одиниці довжини і стала d дифракційної ґратки є оберненими величинами, тобто

У якісних ґраток стала ґратки (період) є малою величиною і вони мають добру роздільну здатність та кутову дисперсію.
3. Контрольні запитання.
1. Яке явище називається дифракцією світла? Яка умова її спостереження?
2. В чому полягає принцип Гюйгенса-Френеля?
3. Які умови спостереження дифракційних максимумів і мінімумів при дифракції на одній щілині?
4. Що являє собою одномірна дифракційна гратка? Яка величина називається сталою (періодом) ґратки?
5. Які дифракційні максимуми називаються головними? Записати і пояснити умови їх спостереження.
6. Яка величина називається роздільною здатністю ґратки? Від чого вона залежить і в яких одиницях виражається?
7. Що називається величиною кутової дисперсії ґратки? Від чого вона залежить і в яких одиницях вимірюється?
8. Яке практичне використання дифракційних ґраток?
9. В чому суть методики виконання даної лабораторної роботи?
Поиск по сайту: